高级语言程序设计I 课堂材料
8 October, 2019上课时间 / 地点: H451, 周二 18: 40, 周四 18: 40
本页面链接有效期至 2019 年 12 月 31 日, 期间可能会在本页面通知页面地址变更.
推荐使用 Chrome, Firefox, Safari, Edge 浏览器打开本页, 不推荐使用 QQ 内置浏览器打开.
课堂材料可从本文内下载, 或由学委转载至班群.
更新时间为每周三 21: 00 前和每周五 21: 00 前 (绝赞持续更新中).
粉碎你的使用说明书
31 July, 2018前几天被别人安利了这个玩意儿 ((制作你的说明书), 打算看看到底是什么货色
其实被各种社交网站刮风搞得有点谜了, 但是看巨佬 @xmcp 有一段时间一刮风就去挖人家老底的操作还是很羡慕的, 所以这次就跟一波风批判一下搞出这个使用书生成器的网易云音乐

网址链接中间有一个随机 ID, 多半是用来检测是谁分享的链接用的, 现在把一个 sample 挂在这里:https://st.music.163.com/c/m2-spec/1abCDEFghi/index.html
退役之前的一些黑照
7 June, 2017算是说已经退役了吧...... 因为 (莫名地考炸好几次所以) 排的太靠后, 所以 D 类买活妥妥地失败了. 不过话说回来要拿金牌才可能有降一本线的政策所以不去也没有关系----这当然是精神胜利法, 不然我实在是不知道如何抚慰我已经受伤的心灵了......

所以就把一些上古时代的照片放上来纪念一下----
Windows 10: Darkened
21 May, 2017In search for a more visually friendly appearance for my computer, I have decided to try out some dark themes.
On Deviantart I discovered a dark theme specially designed for Windows 10 and its derivatives. With some various tweaks and modifications it can achieve an astounding look. This theme, and its affiliated icons, are licensed under GPL and are free to use.
CTSC2017 & APIO2017 游记
15 May, 2017所以说我这样的蒟蒻已经退役了 (大雾), 但是还是要去一波 CTSC&APIO 的, 毕竟是一次难得的做 (tui) 题 (fei) 机会. 虽然说 D 类买活还是参考这两个成绩的, 但是总觉得还不是很靠谱, 所以退役什么的, 也基本已经是铁一般的事实了. 然而古人所谓 “属予作文以记之” 也不过如此, 我便不写滚粗记了, 改写游记, 毕竟这一阵还是很开心的~

这应该说是第一次去 “外地” 参加比赛吧...... 所以对酒店的环境还不是很熟悉. 虽然说各种事情都在意料之中, 不是很奇怪, 但是毕竟是新环境, 还需要一段时间适应.
bzoj4260: Codechef REBXOR
21 April, 2017Description
给定一个含 \(n\) 个元素的数组 \(A\), 下标从 \(1\) 开始. 请找出下面式子的最大值:\[ (A[l_1] \oplus A[l_1+1] \oplus \ldots \oplus A[r_1]) + (A[l_2] \oplus A[l_2+1] \oplus \ldots \oplus A[r_2]) \] 其中 \(1 \leq l_1 \leq r_1 \lt l_2 \leq r_2 \leq n\).
Input
输入数据的第一行包含一个整数 \(n\), 表示数组中的元素个数.
第二行包含 \(n\) 个整数 \(A_1, A_2, \ldots, A_n\).
Output
输出一行包含给定表达式可能的最大值.
bzoj3309: DZY Loves Math
21 April, 2017Description
对于正整数 \(n\), 定义 \(f(n)\) 为 \(n\) 所含质因子的最大幂指数. 例如 \(f(1960) = f(2^3 \times 5^1 \times 7^2) = 3\),\(f(10007) = 1\),\(f(1) = 0\). 现给定正整数 \(a, b\), 求:\[ \sum_{i=1}^{a} \sum_{j=1}^{b} f(gcd(i, j)) \]
Input
第一行一个数 \(T\), 表示询问数.
接下来 \(T\) 行, 每行两个数 \(a, b\), 表示一个询问.
Output
对于每一个询问, 输出一行一个非负整数作为回答.
bzoj1823: [JSOI2010]满汉全席
20 April, 2017Description
满汉全席是中国最丰盛的宴客菜肴, 有许多种不同的材料透过满族或是汉族的料理方式, 呈现在數量繁多的菜色之中. 由于菜色众多而繁杂, 只有极少數博学多闻技艺高超的厨师能够做出满汉全席, 而能够烹饪出经过专家认证的满汉全席, 也是中国厨师最大的荣誉之一. 世界满汉全席协会是由能够料理满汉全席的专家厨师们所组成, 而他们之间还细分为许多不同等级的厨师. 为了招收新进的厨师进入世界满汉全席协会, 将于近日举办满汉全席大赛, 协会派遣许多会员当作评审员, 为的就是要在參赛的厨师之中, 找到满汉料理界的明日之星.
大会的规则如下: 每位參赛的选手可以得到 \(n\) 种材料, 选手可以自由选择用满式或是汉式料理将材料当成菜肴. 大会的评审制度是: 共有 \(m\) 位评审员分别把关. 每一位评审员对于满汉全席有各自独特的見解, 但基本见解是, 要有兩样菜色作为满汉全席的标志. 如某评审认为, 如果没有汉式东坡肉跟满式的涮羊肉锅, 就不能算是满汉全席. 但避免过于有主見的审核, 大会规定一个评审员除非是在认为必备的两样菜色都没有做出來的狀况下, 才能淘汰一位选手, 否则不能淘汰一位參赛者. 换句话說, 只要參赛者能在这兩种材料的做法中, 其中一个符合评审的喜好即可通过该评审的审查. 如材料有猪肉, 羊肉和牛肉时, 有四位评审员的喜好如下表:
| 评审一 | 评审二 | 评审三 | 评审四 |
|---|---|---|---|
| 满式牛肉 | 满式猪肉 | 汉式牛肉 | 汉式牛肉 |
| 汉式猪肉 | 满式羊肉 | 汉式猪肉 | 满式羊肉 |
如參赛者甲做出满式猪肉, 满式羊肉和满式牛肉料理, 他将无法满足评审三的要求, 无法通过评审. 而參赛者乙做出汉式猪肉, 满式羊肉和满式牛肉料理, 就可以满足所有评审的要求. 但大会后來发现, 在这样的制度下如果材料选择跟派出的评审员没有特别安排好的话, 所有的參赛者最多只能通过部分评审员的审查而不是全部, 所以可能会发生没有人通过考核的情形.
如有四个评审员喜好如下表时, 则不論參赛者采取什么样的做法, 都不可能通过所有评审的考核:
| 评审一 | 评审二 | 评审三 | 评审四 |
|---|---|---|---|
| 满式羊肉 | 满式猪肉 | 汉式羊肉 | 汉式羊肉 |
| 汉式猪肉 | 满式羊肉 | 汉式猪肉 | 满式猪肉 |
所以大会希望有人能写一个程序判断, 所选出的 \(m\) 位评审, 会不会发生没有人能通过考核的窘境, 以便协会组织合适的评审团.
Input
第一行包含一个数字 \(k\), 代表测试文件包含了 \(k\) 组资料.
每一组测试资料的第一行包含兩个数字 \(n, m\), 代表有 \(n\) 种材料,\(m\) 位评审员. 为方便起見, 材料舍弃中文名称而给予编号, 编号分别从 \(1\) 到 \(n\).
接下來的 \(m\) 行, 每行都代表对应的评审员所拥有的兩个喜好, 每个喜好由一个英文字母跟一个数字代表, 如 \(m1\) 代表这个评审喜欢第 \(1\) 个材料透过满式料理做出來的菜, 而 \(h2\) 代表这个评审员喜欢第 \(2\) 个材料透过汉式料理做出來的菜.
Output
每组测试资料输出一行, 如果不会发生没有人能通过考核的窘境, 输出 GOOD; 否则输出 BAD.
bzoj3563: DZY Loves Chinese
20 April, 2017Description
神校 XJ 之学霸兮, Dzy 皇考曰 JC.
摄提贞于孟陬兮, 惟庚寅 Dzy 以降.
纷 Dzy 既有此内美兮, 又重之以修能.
遂降临于 OI 界, 欲以神力而凌♂辱众生.
今 Dzy 有一魞歄图, 其上有 \(n\) 座祭坛, 又有 \(m\) 条膴蠁边.
时而 Dzy 狂 WA 而怒发冲冠, 神力外溢, 遂有 \(k\) 条膴蠁边灰飞烟灭.
而后俟其日 A50 题则又令其复原. (可视为立即复原)
然若有祭坛无法相互到达, Dzy 之神力便会大减, 于是欲知其是否连通.
Input
第一行 \(n, m\)
接下来 \(m\) 行 \(x, y\): 表示 \(m\) 条膴蠁边, 依次编号
接下来一行 \(Q\)
接下来 \(Q\) 行:
每行第一个数 \(k\) 而后 \(k\) 个编号 \(c_1 \sim c_k\): 表示 \(k\) 条边, 编号为 \(c_1 \sim c_k\)
为了体现在线,\(k\) 以及 \(c_1 \sim c_k\) 均需异或之前回答为连通的个数
Output
对于每个询问输出: 连通则为 “Connected”, 不连通则为 “Disconnected” (不加引号).
bzoj3569: DZY Loves Chinese II
20 April, 2017Description
神校 XJ 之学霸兮, Dzy 皇考曰 JC.
摄提贞于孟陬兮, 惟庚寅 Dzy 以降.
纷 Dzy 既有此内美兮, 又重之以修能.
遂降临于 OI 界, 欲以神力而凌♂辱众生.
今 Dzy 有一魞歄图, 其上有 \(n\) 座祭坛, 又有 \(m\) 条膴蠁边.
时而 Dzy 狂 WA 而怒发冲冠, 神力外溢, 遂有 \(k\) 条膴蠁边灰飞烟灭.
而后俟其日 A50 题则又令其复原. (可视为立即复原)
然若有祭坛无法相互到达, Dzy 之神力便会大减, 于是欲知其是否连通.
Input
第一行 \(n, m\)
接下来 \(m\) 行 \(x, y\): 表示 \(m\) 条膴蠁边, 依次编号
接下来一行 \(Q\)
接下来 \(Q\) 行:
每行第一个数 \(k\) 而后 \(k\) 个编号 \(c_1 \sim c_k\): 表示 \(k\) 条边, 编号为 \(c_1 \sim c_k\)
为了体现在线,\(c_1 \sim c_k\) 均需异或之前回答为连通的个数
Output
对于每个询问输出: 连通则为 “Connected”, 不连通则为 “Disconnected” (不加引号).
bzoj1822: [JSOI2010]Frozen Nova 冷冻波
20 April, 2017Description
WJJ 喜欢 “魔兽争霸” 这个游戏. 在游戏中, 巫妖是一种强大的英雄, 它的技能 Frozen Nova 每次可以杀死一个小精灵. 我们认为, 巫妖和小精灵都可以看成是平面上的点. 当巫妖和小精灵之间的直线距离不超过 \(R\), 且巫妖看到小精灵的视线没有被树木阻挡 (也就是说, 巫妖和小精灵的连线与任何树木都没有公共点) 的话, 巫妖就可以瞬间杀灭一个小精灵. 在森林里有 \(n\) 个巫妖, 每个巫妖释放 Frozen Nova 之后, 都需要等待一段时间, 才能再次施放. 不同的巫妖有不同的等待时间和施法范围, 但相同的是, 每次施放都可以杀死一个小精灵. 现在巫妖的头目想知道, 若从 \(0\) 时刻开始计算, 至少需要花费多少时间, 可以杀死所有的小精灵?
Input
输入文件第一行包含三个整数 \(n, m, k\), 分别代表巫妖的数量、小精灵的数量和树木的数量.
接下来 \(n\) 行, 每行包含四个整数 \(x, y, r, t\), 分别代表了每个巫妖的坐标、攻击范围和施法间隔 (单位为秒).
再接下来 \(m\) 行, 每行两个整数 \(x, y\), 分别代表了每个小精灵的坐标.
再接下来 \(k\) 行, 每行三个整数 \(x, y, r\), 分别代表了每个树木的坐标.
Output
输出一行, 为消灭所有小精灵的最短时间 (以秒计算). 如果永远无法消灭所有的小精灵, 则输出-1.
bzoj1824: [JSOI2010]下棋问题
20 April, 2017Description
JYY 发明了一个新的益智游戏, 该游戏由 A 和 B兩人轮流在一个 \(10^6 \times 10^6\) 的方格棋盘上的网格线交点下棋, 网格线交点的坐标以 \((x, y)\) 表示之,\((0, 0)\) 代表棋盘最左下角的点. 每一个棋子放置的位置不可以与任何其它棋子在同一 \(X\) 坐标或 \(Y\) 坐标上, 棋盘上新增加一个棋子时, 棋盘上的计数器会自动算出以目前棋盘上棋子所能够围成的 “无障碍四方形” 个数. “无障碍四方形” 是指以任意兩个棋子所定义出的四方形内部不含其它棋子, 每下一个棋子后所算出的 “无障碍四方形” 个数即为下该棋子的得分数. 每位下棋者的总分即是该下棋者每个所下棋子的得分数总和. 请写一个程序计算 A 和 B兩位下棋者的累计总分.
Input
第一行输入只有一个整数 \(n\), 代表此盘棋共下了 \(n\) 个棋子.
接下來的 \(n\) 行, 每一行有兩个整数, 依序代表这 \(n\) 个棋子所放置的位置.
Output
请输出兩个整数, 分别代表该盘棋兩位下棋者的累计得分數. 先下棋者 (A) 的分数在前, 后下棋者 (B) 的分数在后, 中间用一个空格隔开.
bzoj1826: [JSOI2010]缓存交换
19 April, 2017Description
在计算机中, CPU 只能和高速缓存 Cache 直接交换数据. 当所需的内存单元不在 Cache 中时, 则需要从主存里把数据调入 Cache. 此时, 如果 Cache 容量已满, 则必须先从中删除一个.
例如, 当前 Cache 容量为 \(3\), 且已经有编号为 \(10\) 和 \(20\) 的主存单元. 此时, CPU 访问编号为 \(10\) 的主存单元, Cache 命中. 接着, CPU 访问编号为 \(21\) 的主存单元, 那么只需将该主存单元移入 Cache 中, 造成一次缺失 (Cache Miss). 接着, CPU 访问编号为 \(31\) 的主存单元, 则必须从 Cache 中换出一块, 才能将编号为 \(31\) 的主存单元移入 Cache, 假设我们移出了编号为 \(10\) 的主存单元. 接着, CPU 再次访问编号为 \(10\) 的主存单元, 则又引起了一次缺失. 我们看到, 如果在上一次删除时, 删除其他的单元, 则可以避免本次访问的缺失. 在现代计算机中, 往往采用 LRU (最近最少使用) 的算法来进行 Cache 调度----可是, 从上一个例子就能看出, 这并不是最优的算法.
对于一个固定容量的空 Cache 和连续的若干主存访问请求, 聪聪想知道如何在每次 Cache 缺失时换出正确的主存单元, 以达到最少的 Cache 缺失次数.
Input
输入文件第一行包含两个整数 \(n\) 和 \(m\), 分别代表了主存访问的次数和 Cache 的容量.
第二行包含了 \(n\) 个空格分开的正整数, 按访问请求先后顺序给出了每个主存块的编号 (不超过 \(10^9\)) .
Output
输出一行, 为 Cache 缺失次数的最小值.
bzoj1821: [JSOI2010]Group 部落划分 Group
19 April, 2017Description
聪聪研究发现, 荒岛野人总是过着群居的生活, 但是, 并不是整个荒岛上的所有野人都属于同一个部落, 野人们总是拉帮结派形成属于自己的部落, 不同的部落之间则经常发生争斗. 只是, 这一切都成为谜团了----聪聪根本就不知道部落究竟是如何分布的.
不过好消息是, 聪聪得到了一份荒岛的地图. 地图上标注了 \(n\) 个野人居住的地点 (可以看作是平面上的坐标). 我们知道, 同一个部落的野人总是生活在附近. 我们把两个部落的距离, 定义为部落中距离最近的那两个居住点的距离. 聪聪还获得了一个有意义的信息----这些野人总共被分为了 \(k\) 个部落! 这真是个好消息. 聪聪希望从这些信息里挖掘出所有部落的详细信息. 他正在尝试这样一种算法:
对于任意一种部落划分的方法, 都能够求出两个部落之间的距离, 聪聪希望求出一种部落划分的方法, 使靠得最近的两个部落尽可能远离. 例如, 下面的左图表示了一个好的划分, 而右图则不是. 请你编程帮助聪聪解决这个难题.
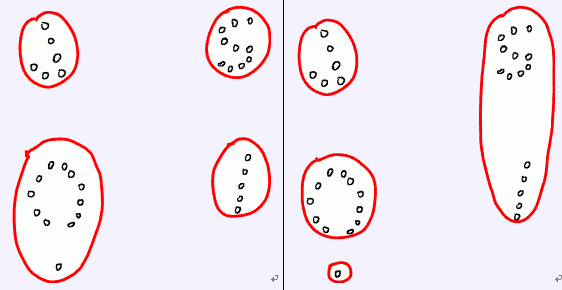
Input
第一行包含两个整数 \(n\) 和 \(k\), 分别代表了野人居住点的数量和部落的数量.
接下来 \(n\) 行, 每行包含两个正整数 \(x, y\), 描述了一个居住点的坐标 \((0 \leq x, y \leq 10000)\).
Output
输出一行, 为最优划分时, 最近的两个部落的距离, 精确到小数点后两位.
bzoj1820: [JSOI2010]Express Service 快递服务
19 April, 2017Description
「飞奔」快递公司成立之后, 已经分别与市内许多中小企业公司签订邮件收送服务契约. 由于有些公司是在同一栋大楼内, 所以「飞奔」公司收件的地点 (收件点) 最多只有 \(m\) 点 \((1, 2, \ldots, m)\), 因此「飞奔」仅先行采购了三辆货車并聘用了三名司机, 每天早上分别从收件地点 \(1, 2\) 及 \(3\) 出发. 而在与客户的服务契约中有明确订约: 「飞奔」必须在客户提出邮件寄送要求的隔天派人至该公司 (地点) 收件.
为了能更有效率的服务客户并节省收件时间, 该公司设立了收件服务登记网站, 客户如有邮件需要寄送, 必须在需要收件的前一天就先上网登记. 为了节省油量, 「飞奔」就利用晚上先行安排三位司机隔天的收件路线. 每位司机至各地点收件的顺序应与各公司上网登记的顺序相符且必须能在最省油的情况下完成当天所有的收件服务. 因此每位司机有可能需要在不同时间重复到同一地点收件, 或不同的司机有可能需在不同的时间点前往同一地点收件.
如下面范例二: 收件公司地点依序为:\(4, 2, 4, 1, 5, 4, 3, 2, 1\) 所示, 虽然司机 \(1\) 一开始就已经在收件地点 \(1\) 了, 但是他却不能先把后面第四个登记的公司 (地点 \(1\)) 邮件先收了再前往第一、第二、或第三个登记收件地点 (地点 \(4, 2, 4\)) 收件. 但是如果前三个登记收件的服务是由司机 \(2\) 或 \(3\) 來负责, 则司机 \(1\) 就可以在地点 \(1\) 收了第四个登记的邮件后再前往后面所登记的地点收件.
此外, 在某些情况下, 不一定每辆车都要收到货, 也就是說, 最佳收件方式也有可能是只需出动一或兩辆车去收货. 请写一个程序來帮「飞奔」公司计算每天依预约顺序至各收件地点收件的最少总耗油量.
Input
输入文件第一行有一个整数 \(m (3 \leq m \leq 200)\), 代表「飞奔」公司收件的地点数, 以 \(1\) 至 \(m\) 之间的整数代号來表示每个地点.
接下來的 \(m\) 行 (第 \(2\) 到第 \(m+1\) 行), 每行有 \(m\) 个整数, 代表一个矩阵 \(D\). 第 \(i +1\) 行的第 \(j\) 个整数是 \(D(i, j)\),\(D(i, j)\) 代表司机开车从收件点 \(i\) 到收件点 \(j\) 所需耗油量.
最后有一行数串, 数串之数字依序为前一天上网登记要求收件的公司地点代号, 最多会有 \(1000\) 个收件请求. 输入文件中任兩个相邻的整数都以一个空白隔开.
Output
输出一个整数, 代表收件所需最少总耗油量.
bzoj1065: [NOI2008]奥运物流
19 April, 2017Description
2008 北京奥运会即将开幕, 举国上下都在为这一盛事做好准备. 为了高效率、成功地举办奥运会, 对物流系统进行规划是必不可少的.
物流系统由若干物流基站组成, 以 \(1 \ldots n\) 进行编号. 每个物流基站 \(i\) 都有且仅有一个后继基站 \(S_i\), 而可以有多个前驱基站. 基站 \(i\) 中需要继续运输的物资都将被运往后继基站 \(S_i\), 显然一个物流基站的后继基站不能是其本身. 编号为 \(1\) 的物流基站称为控制基站, 从任何物流基站都可将物资运往控制基站. 注意控制基站也有后继基站, 以便在需要时进行物资的流通. 在物流系统中, 高可靠性与低成本是主要设计目. 对于基站 \(i\), 我们定义其 “可靠性”\(R(i)\) 如下:
设物流基站 \(i\) 有 \(w\) 个前驱基站 \(P_1, P_2, \ldots, P_w\), 即这些基站以 \(i\) 为后继基站, 则基站 \(i\) 的可靠性 \(R(i)\) 满足下式:
\[ R(i) = C_i + k \sum_{j=1}^{w} R(P_j) \]
其中 \(C_i\) 和 \(k\) 都是常实数且恒为正, 且有 \(k\) 小于 \(1\).
整个系统的可靠性与控制基站的可靠性正相关, 我们的目标是通过修改物流系统, 即更改某些基站的后继基站, 使得控制基站的可靠性 \(R(1)\) 尽量大. 但由于经费限制, 最多只能修改 \(m\) 个基站的后继基站, 并且, 控制基站的后继基站不可被修改. 因而我们所面临的问题就是, 如何修改不超过 \(m\) 个基站的后继, 使得控制基站的可靠性 \(R(1)\) 最大化.
Input
输入第一行包含两个整数与一个实数,\(n, m, k\). 其中 \(n\) 表示基站数目,\(m\) 表示最多可修改的后继基站数目,\(k\) 分别为可靠性定义中的常数.
第二行包含 \(n\) 个整数, 分别是 \(S_1, S_2, \ldots, S_n\), 即每一个基站的后继基站编号.
第三行包含 \(n\) 个正实数, 分别是 \(C_1, C_2, \ldots, C_n\), 为可靠性定义中的常数.
Output
输出仅包含一个实数, 为可得到的最大 \(R(1)\). 精确到小数点两位.