高级打字机 (type. cpp/c/pas)
题目描述
早苗入手了最新的高级打字机. 最新款自然有着与以往不同的功能, 那就是它具备撤销功能, 厉害吧.
请为这种高级打字机设计一个程序, 支持如下 3 种操作:
T x: 在文章末尾打下一个小写字母 x. (Type 操作)U x: 撤销最后的 x 次修改操作. (Undo 操作, 注意 Query 操作并不算修改操作)Q x: 询问当前文章中第 x 个字母并输出. (Query 操作)
文章一开始可以视为空串.
输入格式
第 1 行: 一个整数 n, 表示操作数量.
以下 n 行, 每行一个命令. 保证输入的命令合法.
输出格式
每行输出一个字母, 表示 Query 操作的答案.
样例输入
7
T a
T b
T c
Q 2
U 2
T c
Q 2样例输出
b
c数据范围
对于 40% 的数据 \(n \leq 200\);
对于 100% 的数据 \(n \leq 100000\); 保证 Undo 操作不会撤销 Undo 操作.
高级挑战
对于 200% 的数据 \(n \leq 100000\); Undo 操作可以撤销 Undo 操作.
IOI 挑战
必须使用在线算法完成该题.
Explanation
题目有这样几种解法:
- 直接暴力每次枚举, 然后可能就是一个 \(O(n^3)\) 之类的做法, 可以过 40% 的数据.
- 用堆来维护暴力枚举, 这样是一个 \(O(n)\) 的做法, 但是 Undo 操作不可以撤销 Undo 操作.
- 用 DFS 序来维护这样一棵可持久化的树等等, 具体见官方题解如下:
本题虽为 2012 年 IOI 的题目, 但只要使用离线算法, 就成为只需 noip 级别编程水平的题目了.
以下声明一些定义: (对于此类题目以及各种可持久化数据结构的离线解法的思考很有帮助)
版本: 接受第 1--i 个修改操作 (包含 Type 和 Undo) 后的状态称为版本 i. 版本 0 为初始状态.
版本链: 一般的数据结构题目只有各种修改命令 (比如本题的 Type 操作), 那么所有版本就会呈链状排列.
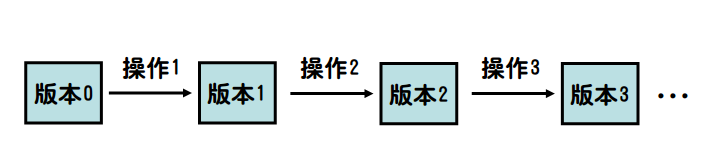
这种情况下只需要设计一个合理的数据结构依次执行操作即可.
版本树:Undo x 撤销最近的 x 次修改操作, 实际上就是当前版本还原为 x 次操作前的版本, 换句话说, 版本 i=版本 i-x-1.
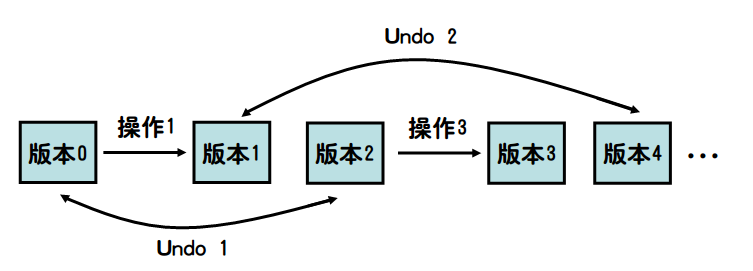
如图所示, 所有版本呈树状排列, 版本 0 为根.
读入所有操作并建树, 对这颗版本树按欧拉序求出所有版本. 上图中就是按 0->1->4...... 4->1->0->2->3->2->0 的顺序遍历, 同样使用栈就能计算出所有的版本, 然后在对应的版本上解决询问即可.
到此, 就得到了时空复杂度均为 O (n) 的离线算法.
能解决这类题目的条件是:
- 允许使用离线算法, 进而求出版本树, 并允许把询问挂到树的节点上.
- 所有操作都是可逆的. 只有所有操作都是可逆的, 才能按欧拉序依次求出各版本. 如本题的 Type 操作的逆操作就是弹出栈顶, Undo 操作则根本不需要修改 (Undo 前后 2 个版本相同).
相关题目: crisis 60% (2012 国家集训队 hw2 出题互测/卓亮)
| IOI 挑战 | 算法复杂度 |
|---|---|
| Trie+倍增法寻祖 | \(O(n \cdot log(n))\) |
| 各种可持久化数据结构: 可持久化块状数组 | \(O(n \cdot \sqrt{n})\) |
| 可持久化跳表 (与 Trie 解法相近) | \(O(n \cdot log(n))\) |
因超出 noip 范围不做更多展开.
然而总数居里只有 50% 是 100% 分做法, 最后只能强行写 DFS 序了~
Source Code
100% 解法
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn = 100100;
// Attempted to create an abstruse name...
class EulerTraversal
{
public:
char data[maxn], // Static data of Type() functions
stk[maxn]; // Temporary stack
int pend_answer[maxn], // Pended answer for final dump. Do not use CHAR!
par[maxn]; // Node parent
// A in-verbose graph implementation from scratch
int graph_edges[maxn], // FIXME:???
graph_next[maxn], // FIXME:???
graph_to[maxn]; // FIXME:???
vector<int> pend_queries[maxn]; // Inserts # of queries
int data_idx, edge_idx, pend_ans_idx;
void insert_edge(int u, int v)
{
int p = ++edge_idx; // Assigned new edge id
// Literally... addedge(u, v).
graph_next[p] = graph_edges[u];
graph_edges[u] = p;
graph_to[p] = v;
return ;
}
void pend_type(char ch)
{
// Set original data with ch.
data[data_idx] = ch;
data_idx++; // and update id / count
// Link parent to direct parent (as in the chain)
par[data_idx] = data_idx - 1;
return ;
}
void pend_undo(int steps)
{
data_idx++;
int parent = data_idx - steps - 1;
this->insert_edge(parent, data_idx);
par[data_idx] = parent;
return ;
}
void pend_query(int pos)
{
// Assign a new index for this query id.
pend_queries[data_idx].push_back(++pend_ans_idx);
// The pended answer is now the query param, and will be updated
// in eval() function.
pend_answer[pend_ans_idx] = pos;
return ;
}
void eval(void)
{
int pos = 0; // Current stack pointer
for (int p = 0; ; ) { // p starts from root
if (graph_edges[p]) {
int v = graph_to[graph_edges[p]];
// Remove this 'undo' operation from graph.
graph_edges[p] = graph_next[graph_edges[p]];
// Go to target (i.e. linked undo parent), forcefully.
p = v; continue;
}
// If current position is on the chain
if (data[p] != (char)0) {
// Append type operation to stack
stk[++pos] = data[p];
// Mark original data as used (no duplications, guranteed)
data[p] = 0;
// Increment / traverse to child... forcefully.
p++; continue;
}
// Flush results to node queries
for (unsigned int i = 0; i < pend_queries[p].size(); i++) {
// v is the assigned query id.
int v = pend_queries[p][i];
// As it is, the original value is the param, i.e. query(...[v])
// which will be converted into actual datum.
pend_answer[v] = stk[pend_answer[v]];
}
// Traverse to parent if is on a chain
if (par[p] + 1 == p)
pos--; // Pop in stack
// Break when reached root
if (p == 0)
return ;
p = par[p];
}
return ;
}
void flush(void)
{
// Flush pre-calculated answers
for (int i = 1; i <= pend_ans_idx; i++)
printf("%c\n", pend_answer[i]);
return ;
}
} graph;
int n;
int main(int argc, char** argv)
{
scanf("%d", &n);
// Process the operations offline.
// Online implementation is **WAY HARDER** to write!
for (int idx = 1; idx <= n; idx++) {
char str1[64], str2[64];
int tmp1;
scanf("%s", str1);
if (str1[0] == 'T') {
scanf("%s", str2);
graph.pend_type(str2[0]);
} else if (str1[0] == 'U') {
scanf("%d", &tmp1);
graph.pend_undo(tmp1);
} else if (str1[0] == 'Q') {
scanf("%d", &tmp1);
graph.pend_query(tmp1);
}
}
graph.eval();
// Flushing results in buffer
graph.flush();
return 0;
}50% 解法
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
const int maxn = 100100;
char stk[maxn];
int n, top;
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int idx = 1; idx <= n; idx++) {
char str1[64], str2[64];
int tmp1;
scanf("%s", str1);
if (str1[0] == 'T') {
scanf("%s", str2);
stk[++top] = str2[0];
} else if (str1[0] == 'U') {
scanf("%d", &tmp1);
top = max(0, top - tmp1);
} else if (str1[0] == 'Q') {
scanf("%d", &tmp1);
printf("%c\n", stk[tmp1]);
}
}
return 0;
}