不等数列 (num. cpp/c/pas)
题目描述
将 1 到 n 任意排列, 然后在排列的每两个数之间根据他们的大小关系插入 “>” 和 “<” . 问在所有排列中, 有多少个排列恰好有 k 个 “<” . 答案对 2012 取模.
输入格式
第一行 2 个整数 n, k.
输出格式
一个整数表示答案.
样例输入
5 2样例输出
66数据范围
对于 30% 的数据:\(n \leq 10\)
对于 100% 的数据:\(k \lt n \leq 1000\)
Explanation
想法和正解一样, 所以只贴官方题解:
对于 30%\(n \leq 10\) 的数据, 搜索打表, 状态压缩动态规划......
对于 1--n 等类似的排列计数问题, 以动态规划和组合数学 2 种大方向为基本解决方向.
组合数学在 noip 最难也就到杨辉三角左右, 所以这题我从动态规划展开.
如果此类排列问题在脑中的模型是: “有 n 个格子, 填入 1--n”, 那么相对应的 DP 就不得不记录哪些数填过了 (从左到右填入) 或者哪些格子填过了 (从小到大填入). 这样一来就必须要使用状态压缩来存储这些信息, 就使得复杂度变得难以接受.
而如果换个模型: “从小到大把数字插入数列”. 注意是数列而不是格子, 这样一来就不需要 记录是哪些数字插入了 (而只要记录插入到了第几个数字), 同时不需要记录每个数字的具体位置, 也不需要记录数字的相对位置, 而只需记录相对关系的数目 (对本题而言就是有几个 “<” ).
因为是从小到大插入数字, 所以当前插入的数字一定大于所有已经插入的.
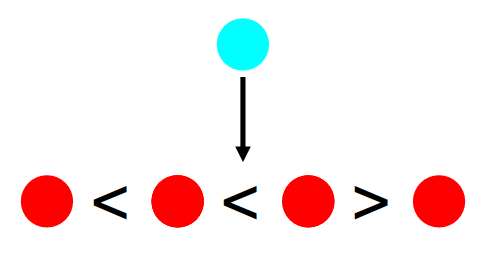
蓝色是当前插入的数字, 如果它插入到<关系的 2 个数字之间 (或者数列最左端), 就会使数 列的 `<` 数量不变, `>` 数量+1:
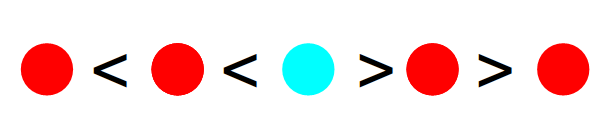
类似的, 插入到>关系的 2 个数字之间 (或者数列最右端), 数列的<数量+1, >数量不变.
F [i] [j] 表示前 i 个数字构成的数列中, 恰有 j 个 ‘<’ 号的方案数 (‘>’ 号就有 i-j-1 个).
F [i] [j]=F [i-1] [j-1] (i-j)+F [i-1] [j] (j+1).
时空复杂度:\(O(n^2)\)
若打表则时间复杂度为 \(O(1)\)
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
const int maxn = 1010, modr = 2012;
int n, k;
int dp[maxn][maxn];
int main(int argc, char** argv)
{
scanf("%d%d", &n, &k);
// We choose to use dp... because:
// Given a sequence of n - 1 numbers, of a permutation of (1..n-1):
// It appears that when you insert the number n into this sequence, it
// would provide both < and > signs when in the middle of the sequence,
// a > at the begin of the sequence and a < at the end of the sequence.
// We can use this to optimize the dynamic programming procedure.
dp[1][0] = 1; // That's comprehensive...
dp[2][0] = 1;
dp[2][1] = 1; // To avoid boundaries judging in the main.
for (int i = 3; i <= n; i++) {
dp[i][0] = 1;
for (int j = 0; j <= i - 1; j++)
dp[i][j] = (dp[i - 1][j - 1] * (i - j) // Those with > signs
+ dp[i - 1][j] * (j + 1)) // Those with < signs
% modr;
continue;
}
printf("%d\n", dp[n][k]);
return 0;
}