题目描述
有 n 个同学 (编号为 1 到 n) 正在玩一个信息传递的游戏. 在游戏里每人都有一个固定的信息传递对象, 其中, 编号为 i 的同学的信息传递对象是编号为 Ti 同学.
游戏开始时, 每人都只知道自己的生日. 之后每一轮中, 所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象 (注意: 可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人, 即自己的信息传递对象). 当有人从别人口中得知自己的生日时, 游戏结束. 请问该游戏一共可以进行几轮?
输入格式
输入共 2 行.
第 1 行包含 1 个正整数 n 表示 n 个人.
第 2 行包含 n 个用空格隔开的正整数 T1, T2, ……, Tn 其中第 i 个整数 Ti 示编号为 i 的同学的信息传递对象是编号为 Ti 的同学, Ti≤n 且 Ti≠i
数据保证游戏一定会结束.
输出格式
输出共 1 行, 包含 1 个整数, 表示游戏一共可以进行多少轮.
输入样例
5
2 4 2 3 1输出样例
3说明
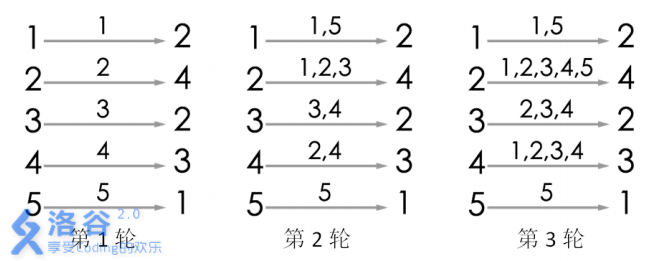
游戏的流程如图所示. 当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自己的生日, 所以答案为 3. 当然, 第 3 轮游戏后, 2 号玩家、3 号玩家都能从自己的消息来源得知自己的生日, 同样符合游戏结束的条件.
对于 30% 的数据,\(n \leq 200\);
对于 60% 的数据,\(n \leq 2500\);
对于 100% 的数据,\(n \leq 200000\).
Explanation
就是说一条单向图 (类树型). 然后环只能进, 不能出. 所以在上面打一个标记就可以了.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <queue>
using namespace std;
typedef long long lli;
const int maxn = 200100;
const int infinit = 0x007f7f7f;
int n;
int to[maxn];
int flag[maxn]; // Whose?
int depth[maxn]; // The depth of the ring iteration.
int res = infinit;
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &to[i]);
// Deep-first searching...
for (int i = 1; i <= n; i++) {
if (flag[i])
continue;
// This means this is a new node...
queue<int> que;
que.push(i);
depth[i] = 1;
while (!que.empty()) {
int p = que.front();
que.pop();
flag[p] = i;
// If this has been reached before...
if (flag[to[p]] < i && flag[to[p]] > 0) {
break;
} else if (flag[to[p]] == i) {
res = min(res, depth[p] - depth[to[p]] + 1);
break;
}
depth[to[p]] = depth[p] + 1;
que.push(to[p]);
// printf("dfsing %d @ %d -> %d\n", i, p, to[p]);
}
}
printf("%d\n", res);
return 0;
}