Description
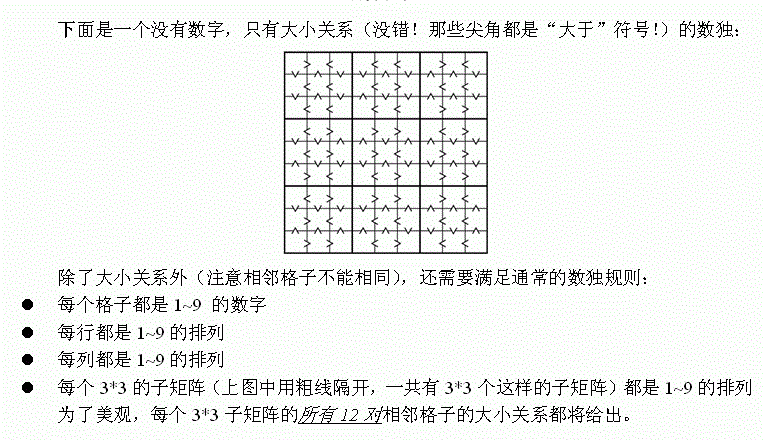
Input
输入一共 15 行, 包含一个新数独的实例. 第奇数行包含左右方向的符号 (< 和>) , 第偶数行包含上下方向的符号 (^ 和v) .
Output
输出包含 9 行, 每行 9 个 1~ 9 的数字, 以单个空格隔开. 输入保证解惟一.
Sample Input
< > > < > <
v v ^ ^ v v ^ ^ ^
< < > < > <
^ ^ ^ v ^ ^ ^ v v
< < < < > >
> < > > > >
v ^ ^ ^ ^ v v v ^
> > > > < >
v v ^ v ^ v ^ v ^
> < < > > >
< < < < > <
v ^ v v v v ^ ^ v
< > > < < >
^ v v v ^ v ^ v v
< > < > < >Sample Output
4 9 1 7 3 6 5 2 8
2 3 7 8 1 5 6 4 9
5 6 8 2 4 9 7 3 1
9 1 3 6 5 4 8 7 2
8 5 4 9 7 2 1 6 3
7 2 6 3 8 1 9 5 4
3 4 9 5 6 8 2 1 7
1 8 5 4 2 7 3 9 6
6 7 2 1 9 3 4 8 5Solution
其实这道题重点在于读数据 (数据太难读了 233)
然后题目的做法就和普通的 DFS 数独没有什么差别了, 大概 1. 3 秒左右能够跑完.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
typedef long long lli;
const int maxn = 12;
#define ARROW_UP '^'
#define ARROW_LF '<'
#define ARROW_RT '>'
#define ARROW_DN 'v'
const int grid[10][10] = {
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 1, 1, 2, 2, 2, 3, 3, 3,
0, 1, 1, 1, 2, 2, 2, 3, 3, 3,
0, 1, 1, 1, 2, 2, 2, 3, 3, 3,
0, 4, 4, 4, 5, 5, 5, 6, 6, 6,
0, 4, 4, 4, 5, 5, 5, 6, 6, 6,
0, 4, 4, 4, 5, 5, 5, 6, 6, 6,
0, 7, 7, 7, 8, 8, 8, 9, 9, 9,
0, 7, 7, 7, 8, 8, 8, 9, 9, 9,
0, 7, 7, 7, 8, 8, 8, 9, 9, 9
};
int map[maxn][maxn][2];
int arr[maxn][maxn];
bool x_lim[maxn][maxn], // Rows
y_lim[maxn][maxn], // Columns
z_lim[maxn][maxn]; // Small 3x3 areas
char get_arrow_char(void) { char ch = '\0';
while (ch != ARROW_UP && ch != ARROW_LF && ch != ARROW_RT && ch != ARROW_DN)
scanf("%c", &ch);
return ch; }
void print_matrix(void) {
for (int i = 1; i <= 9; i++) {
for (int j = 1; j <= 8; j++)
printf("%d ", arr[i][j]);
printf("%d\n", arr[i][9]);
} return ; }
bool dfs_end;
void dfs(int x, int y)
{
// Reached horizontal (rightmost) boundary, skipping to next row
if (y == 10) { x++; y = 1; }
// Reached end of deep first search, getting result.
if (x == 10) { dfs_end = true; print_matrix(); return ; }
// Setting maximum search limits
int l = 1, r = 9;
// If limited by upper block
if (map[x][y][0]) {
if (map[x][y][0] == 1) r = min(r, arr[x - 1][y] - 1);
else l = max(l, arr[x - 1][y] + 1);
}
// If limited by left, adjacent block
if (map[x][y][1]) {
if (map[x][y][1] == 1) r = min(r, arr[x][y - 1] - 1);
else l = max(l, arr[x][y - 1] + 1);
}
// Searching, deeper
for (int i = l; i <= r; i++)
if (!x_lim[x][i] && !y_lim[y][i] && !z_lim[grid[x][y]][i]) {
// Marking to selected / placeholder
x_lim[x][i] = y_lim[y][i] = z_lim[grid[x][y]][i] = true;
arr[x][y] = i;
// Deep first search
dfs(x, y + 1);
if (dfs_end)
return ;
// Unchoose state, a.k.a. resetting
x_lim[x][i] = y_lim[y][i] = z_lim[grid[x][y]][i] = false;
}
return ;
}
int main(int argc, char** argv)
{
// All blocks are only affected by its upper / lower block.
// Reading in data (should be a complicated one)
// 3 big blocks of rows (5 * 5 area)
for (int k = 1; k <= 3; k++) {
char ch = '\0';
// Read first row
for (int i = 1; i <= 3; i++) {
ch = get_arrow_char();
if (ch == ARROW_RT) map[(k-1) * 3 + 1][(i-1)*3 + 2][1] = 1;
else map[(k-1) * 3 + 1][(i-1)*3 + 2][1] = 2;
ch = get_arrow_char();
if (ch == ARROW_RT) map[(k-1) * 3 + 1][(i-1)*3 + 3][1] = 1;
else map[(k-1) * 3 + 1][(i-1)*3 + 3][1] = 2;
}
// Read rows 2 through 5, respectively
for (int i = 2; i <= 3; i++) {
// Vertical connexions
for (int j = 1; j <= 9; j++) {
ch = get_arrow_char();
if (ch == ARROW_UP) map[(k-1) * 3 + i][j][0] = 2;
else map[(k-1) * 3 + i][j][0] = 1;
}
// Horizontal connexions, relatively similar to row #1
for (int j = 1; j <= 3; j++) {
ch = get_arrow_char();
if (ch == ARROW_RT) map[(k-1) * 3 + i][(j-1)*3 + 2][1] = 1;
else map[(k-1) * 3 + i][(j-1)*3 + 2][1] = 2;
ch = get_arrow_char();
if (ch == ARROW_RT) map[(k-1) * 3 + i][(j-1)*3 + 3][1] = 1;
else map[(k-1) * 3 + i][(j-1)*3 + 3][1] = 2;
}
}
}
// Finished a lot of reading.
// Now generating solution.
dfs_end = false;
dfs(1, 1);
// Termination.
return 0;
}