Description
将要读二年级的小 Q 买了一款新型益智玩具----魔幻棋盘, 它是一个 \(n\) 行 \(m\) 列的网格棋盘, 每个格子中均有一个正整数. 棋盘守护者在棋盘的第 \(x\) 行第 \(y\) 列 (行与列均从 \(1\) 开始编号) 并且始终不会移动. 棋盘守护者会进行两种操作:
- 询问: 他会以自己所在位置为基础, 向四周随机扩展出一块大小不定的矩形区域, 向你 询问这一区域内所有数的最大公约数是多少.
- 修改: 他会随意挑选棋盘上的一块矩形区域, 将这一区域内的所有数同时加上一个给定 的整数.
游戏说明书上附有这样一句话 “聪明的小朋友, 当你连续答对 \(19930324\) 次询问后会得到一个惊喜噢!”“. 小 Q 十分想得到这个惊喜, 于是每天都在玩这个玩具. 但由于他粗心大意, 经常算错数, 难以达到这个目标. 于是他来向你寻求帮助, 希望你帮他写一个程序来回答棋盘守护者的询问, 并保证 100% 的正确率.
为了简化问题, 你的程序只需要完成棋盘守护者的 \(T\) 次操作, 并且问题保证任何时刻 棋盘上的数字均为不超过 \(2^{62}−1\) 的正整数.
Input
第一行为两个正整数 \(n, m\), 表示棋盘的大小;
第二行为两个正整数 \(x, y\), 表示棋盘守护者的位置;
第三行仅有一个正整数 \(T\), 表示棋盘守护者将进行次操作;
接下来 \(n\) 行, 每行有 \(m\) 个正整数, 用来描述初始时棋盘上每个位置的数.
接下来 \(T\) 行, 按操作的时间顺序给出 \(T\) 次操作. 每行描述一次操作, 以一个数字 \(0\) 或 \(1\) 开头:
- 若以数字 \(0\) 开头, 表示此操作为询问, 随后会有四个非负整数 \(x_1, y_1, x_2, y_2\), 表示询问的区域是以棋盘守护者的位置为基础向上扩展 \(x_1\) 行, 向下扩展 \(y_1\) 行, 向左扩展 \(x_2\) 列, 向右扩展 \(y_2\) 列得到的矩形区域 (详见样例).
- 若以数字 \(1\) 开头, 表示此操作为修改, 随后会有四个正整数 \(x_1, y_1, x_2, y_2\) 和一个整数 \(c\), 表示修改区域的上、下边界分别为第 \(x_1, x_2\) 行, 左、右边界分别为第 \(y_1, y_2\) 列 (详见样例), 在此矩形区域内的所有数统一加上 \(c\) (注意 \(c\) 可能为负数).
Output
对于每次询问操作, 每行输出一个数, 表示该区域内所有数的最大公约数.
Sample Input
2 2
1 1
4
6 12
18 24
0 0 0 1 0
1 1 1 1 2 6
1 2 1 2 2 6
0 0 0 1 1Sample Output
6
6Explanation
首先这道题我要 强力™ 吐槽一发, 因为实在是调了太久了=A=
差不多是这样一个痛苦的过程......
- 14 日写出来一个很正常的加法二维线段树模板, 区间查询区间修改, 然后准备魔改 \(gcd(\ldots)\), 瞎搞了一晚上还是没搞出来......
- 15 日看了一篇文章, 突然发现必须是差分维护, 而且有关最大公因子的问题还不能随便区间查询, 不然无法保证 \(O(n \log^2 n)\) 的复杂度, 有可能退化到 \(O(n^2)\), 于是 辛辛苦苦改了一个小时左右弄成单点查询, 再加上各种魔改~ 最后终于把差分的维护 搞定了, 然后果断 WA
- 16 日一整天都在折腾线段树上的问题, 发现实在问题多多, 第二次写指针 (不是堆) 线段树, 结果错误百出,
query(...)居然还是错的, 然后设上 magic 防止NULL爆炸等等, 最后终于把样例过掉了. 突然发现神奇的事发生了, 随机生成器随随便便搞出五组数据里都有一组都是错的, 然后 Back To Debugging 无果, 无奈离开 - 返回来对着正解的程序查了一遍, 结果发现了一句真理, 叫 ”\(n, m\) 写反见祖宗, 十年 OI 一场空 “”. 这种 \(n, m\) 写反系列我也是不说什么了~ 然后把 magic 去掉, 简单优化一下就在耒阳上交过了...... 后来查了一下随机生成器发现它保证 \(n = m\). ......
现在上题解, 也没有什么, 就是两张图, 请读者自己意会, 因为其实这个并不难理解 (膜 PoPoQQQ 爷的题解):
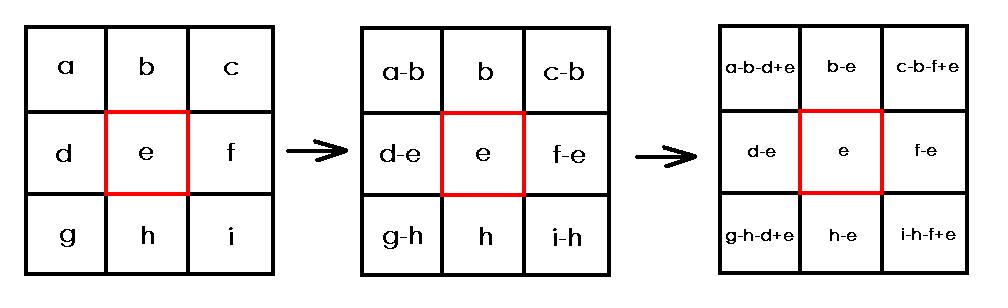
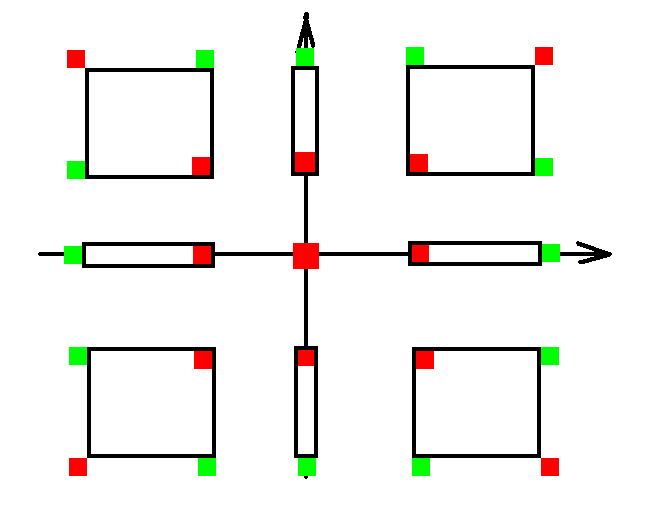
所以说很久都没有写博客了, 然后这道题也是比较老的题了, 毕竟拖了我这么久~
话说 GNU diff 还是很好用的;
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
#define per(_var,_end,_begin) for(int _var=_end;_var>=_begin;_var--)
#define range(_begin,_end) rep(_,_begin,_end)
#define SWTAPI inline
using namespace std;
typedef long long lli;
const int maxn = 500100;
template <typename _T>
class q_array
{
_T arr[maxn];
public:
int n, m;
SWTAPI _T& operator() (int x, int y) {
return arr[(x-1)*m + y];
}
};
SWTAPI lli gcd(lli x, lli y)
{
return __gcd(x, y);
}
class QuadraticSegmentTree
{
public:
struct ynode {
int lb, mb, rb; // Left, middle, right boundaries on y-axis
lli sum; // Data maintainers
ynode *lc, *rc; // children
} ynpool[maxn<<4];
struct xnode {
int lb, mb, rb; // Left, middle, right boundaries
ynode *y_root; // Root on y-axis
xnode *lc, *rc; // children
} xnpool[maxn<<2];
xnode *x_root;
int n, m, yncnt, xncnt;
SWTAPI ynode* make_node_y(void)
{
ynode *p = &ynpool[++yncnt];
p->lb = p->mb = p->rb = 0;
p->sum = 0;
p->lc = p->rc = NULL;
return p;
}
SWTAPI xnode* make_node_x(void)
{
xnode *p = &xnpool[++xncnt];
p->lb = p->mb = p->rb = 0;
p->y_root = NULL;
p->lc = p->rc = NULL;
return p;
}
SWTAPI void update_sum_y(ynode *p)
{
p->sum = gcd(
p->lc->sum,
p->rc->sum );
return ;
}
SWTAPI lli query_y(ynode *p, int lbnd, int rbnd)
{
if (p->lb == lbnd && p->rb == rbnd) {
return p->sum;
}
lli res = 0;
if (rbnd <= p->mb) res = query_y(p->lc, lbnd, rbnd);
else if (lbnd > p->mb) res = query_y(p->rc, lbnd, rbnd);
else res = gcd(
query_y(p->lc, lbnd, p->mb),
query_y(p->rc, p->mb+1, rbnd));
return res;
}
SWTAPI lli query_x(xnode *p, int lbnd, int rbnd, int ubnd, int dbnd)
{
if (p->lb == lbnd && p->rb == rbnd) {
lli res = query_y(p->y_root, ubnd, dbnd);
return res;
}
lli res = 0;
if (rbnd <= p->mb) res = query_x(p->lc, lbnd, rbnd, ubnd, dbnd);
else if (lbnd > p->mb) res = query_x(p->rc, lbnd, rbnd, ubnd, dbnd);
else res = gcd(
query_x(p->lc, lbnd, p->mb, ubnd, dbnd),
query_x(p->rc, p->mb+1, rbnd, ubnd, dbnd));
return res;
}
SWTAPI void change_y(ynode *p, int ypos, lli val)
{
if (p->lb == p->rb) {
p->sum += val;
return ;
}
if (ypos <= p->mb)
change_y(p->lc, ypos, val);
else if (ypos > p->mb)
change_y(p->rc, ypos, val);
update_sum_y(p);
return ;
}
SWTAPI void change_x(xnode *p, int xpos, int ypos, lli val)
{
change_y(p->y_root, ypos, val);
if (p->lb == p->rb) {
return ;
}
if (xpos <= p->mb)
change_x(p->lc, xpos, ypos, val);
else if (xpos > p->mb)
change_x(p->rc, xpos, ypos, val);
// Magic optimizations
lli lval = query_y(p->lc->y_root, ypos, ypos),
rval = query_y(p->rc->y_root, ypos, ypos),
cval = query_y(p->y_root, ypos, ypos);
change_y(p->y_root, ypos, gcd(lval, rval) - cval);
return ;
}
SWTAPI ynode* build_tree_y_init(int l, int r, int x, q_array<lli>& arr)
{
if (l > r) return NULL;
int mid = (l+r)>>1;
ynode *p = make_node_y();
p->lb = l, p->mb = mid, p->rb = r;
if (l == r) {
p->sum = arr(x, mid);
} else {
p->lc = build_tree_y_init(l, mid, x, arr);
p->rc = build_tree_y_init(mid+1, r, x, arr);
p->sum = gcd(p->lc->sum, p->rc->sum);
}
return p;
}
SWTAPI ynode* build_tree_y_comb(int l, int r, ynode* lp, ynode* rp)
{
if (l > r) return NULL;
int mid = (l+r)>>1;
ynode *p = make_node_y();
p->lb = l, p->mb = mid, p->rb = r;
if (l == r) {
p->sum = gcd(lp->sum, rp->sum);
} else if (l != r) {
p->lc = build_tree_y_comb(l, mid, lp->lc, rp->lc);
p->rc = build_tree_y_comb(mid+1, r, lp->rc, rp->rc);
p->sum = gcd(p->lc->sum, p->rc->sum);
}
return p;
}
SWTAPI xnode* build_tree_x(int l, int r, q_array<lli>& arr)
{
if (l > r) return NULL;
int mid = (l+r)>>1;
xnode *p = make_node_x();
p->lb = l, p->mb = mid, p->rb = r;
if (l == r) {
p->y_root = build_tree_y_init(1, m, mid, arr);
} else {
p->lc = build_tree_x(l, mid, arr);
p->rc = build_tree_x(mid+1, r, arr);
// Creating subtree on y-axis, this might be a little painful...
ynode *lc = p->lc->y_root,
*rc = p->rc->y_root;
p->y_root = build_tree_y_comb(1, m, lc, rc);
}
return p;
}
// Public accessors
SWTAPI void change(int x_pos, int y_pos, lli val)
{
change_x(x_root, x_pos, y_pos, val);
return ;
}
SWTAPI lli query(int lbnd, int rbnd, int ubnd, int dbnd)
{
return query_x(x_root, lbnd, rbnd, ubnd, dbnd);
}
SWTAPI void build_tree(q_array<lli>& arr)
{
this->n = arr.n;
this->m = arr.m;
x_root = build_tree_x(1, n, arr);
return ;
}
} st;
q_array<lli> arr;
int n, m, x, y, T;
int main(int argc, char** argv)
{
scanf("%d%d", &n, &m);
scanf("%d%d%d", &x, &y, &T);
arr.n = n, arr.m = m;
rep(i, 1, n) rep(j, 1, m)
scanf("%lld", &arr(i, j));
// Generating differential array.
rep(i, 1, n) {
rep(j, 1, y-1) arr(i, j) -= arr(i, j+1);
per(j, m, y+1) arr(i, j) -= arr(i, j-1);
}
rep(j, 1, m) {
rep(i, 1, x-1) arr(i, j) -= arr(i+1, j);
per(i, n, x+1) arr(i, j) -= arr(i-1, j);
}
// Differential array generated, initializing segment tree.
st.build_tree(arr);
// Processing the queries
for (int idx = 1; idx <= T; idx++) {
int type, x1, x2, y1, y2;
scanf("%d%d%d%d%d", &type, &x1, &y1, &x2, &y2);
if (type == 0) {
lli res = st.query(
x - x1, x + x2,
y - y1, y + y2);
res = abs(res);
printf("%lld\n", res);
} else if (type == 1) {
lli val = 0;
scanf("%lld", &val);
// Top-left corner
if (x1 <= x && x1 > 1 && y1 <= y && y1 > 1)
st.change(x1-1, y1-1, val);
else if (x1 <= x && x1 > 1 && y1 > y )
st.change(x1-1, y1, -val);
else if (x1 > x && y1 <= y && y1 > 1)
st.change(x1, y1-1, -val);
else if (x1 > x && y1 > y)
st.change(x1, y1, val);
// Top-right corner
if (x1 <= x && x1 > 1 && y2 >= y && y2 < m)
st.change(x1-1, y2+1, val);
else if (x1 <= x && x1 > 1 && y2 < y )
st.change(x1-1, y2, -val);
else if (x1 > x && y2 >= y && y2 < m)
st.change(x1, y2+1, -val);
else if (x1 > x && y2 < y)
st.change(x1, y2, val);
// Bottom-left corner
if (x2 >= x && x2 < n && y1 <= y && y1 > 1)
st.change(x2+1, y1-1, val);
else if (x2 < x && y1 <= y && y1 > 1)
st.change(x2, y1-1, -val);
else if (x2 >= x && x2 < n && y1 > y)
st.change(x2+1, y1, -val);
else if (x2 < x && y1 > y)
st.change(x2, y1, val);
// Bottom-right corner
if (x2 >= x && x2 < n && y2 >= y && y2 < m)
st.change(x2+1, y2+1, val);
else if (x2 < x && y2 >= y && y2 < m)
st.change(x2, y2+1, -val);
else if (x2 >= x && x2 < n && y2 < y)
st.change(x2+1, y2, -val);
else if (x2 < x && y2 < y)
st.change(x2, y2, val);
// X-axis edges
if (x1 <= x && x2 >= x) {
// Left edge
if (y1 <= y && y1 > 1)
st.change(x, y1-1, -val);
else if (y1 > y)
st.change(x, y1, val);
// Right edge
if (y2 >= y && y2 < m)
st.change(x, y2+1, -val);
else if (y2 < y)
st.change(x, y2, val);
}
// Y-axis edges
if (y1 <= y && y2 >= y) {
// Top edge
if (x1 <= x && x1 > 1)
st.change(x1-1, y, -val);
else if (x1 > x)
st.change(x1, y, val);
// Bottom edge
if (x2 >= x && x2 < n)
st.change(x2+1, y, -val);
else if (x2 < x)
st.change(x2, y, val);
}
// Centre point
if (x1 <= x && x2 >= x && y1 <= y && y2 >= y)
st.change(x, y, val);
}
}
return 0;
}