Description
到了难得的暑假, 为了庆祝小白在数学考试中取得的优异成绩, 小蓝决定带小白出去旅游~~ 经过一番抉择, 两人决定将 T 国作为他们的目的地. T 国的国土可以用一个凸 \(n\) 边形来表示,\(n\) 个顶点表示 \(n\) 个入境/出境口. T 国包含 \(n-2\) 个城市, 每个城市都是顶点均为 \(n\) 边形顶点的三角形 (换而言之, 城市组成了关于 T 国的一个三角剖分). 两人的旅游路线可以看做是连接 \(n\) 个顶点中不相邻两点的线段.
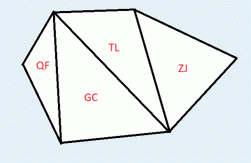
为了能够买到最好的纪念品, 小白希望旅游路线上经过的城市尽量多. 作为小蓝的好友, 你能帮帮小蓝吗?
Input
每个输入文件中仅包含一个测试数据.
第一行包含两个由空格隔开的正整数 \(n\),\(n\) 的含义如题目所述.
接下来有 \(n-2\) 行, 每行包含三个整数 \(p, q, r\), 表示该城市三角形的三个顶点的编号 (T 国的 \(n\) 个顶点按顺时间方向从 \(1\) 至 \(n\) 编号).
Output
输出文件共包含 \(1\) 行, 表示最多经过的城市数目. (一个城市被当做经过当且仅当其与线路有至少两个公共点)
Sample Input
6
1 2 4
2 3 4
1 4 5
1 5 6Sample Output
4Data Range
对于所有数据, 满足:\(4 \leq n \leq 200000\).
Explanation
任意一个凸 \(n\) 边形在三角剖分之后都会得到 \(n-2\) 个三角形.
相邻两个三角形之间有且仅有 \(1\) 条公用边, 一共有 \(n-3\) 条公用边.
于是将公用边当成两个三角形之间的边, 三角形作为新图的节点, 那么新图一定是一棵树.
经过的最多的城市的数目, 就是新图 (树) 的直径了.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long lli;
const int maxn = 200100;
class Graph
{
public:
struct edge
{
int u, v;
edge *next;
};
int n, ecnt, root;
edge *edges[maxn], epool[maxn * 6];
void add_edge(int u, int v)
{
edge *p = &epool[++ecnt],
*q = &epool[++ecnt];
p->u = u; p->v = v;
p->next = edges[u]; edges[u] = p;
q->u = v; q->v = u;
q->next = edges[v]; edges[v] = q;
return ;
}
int par[maxn], depth[maxn];
void dfs(int p)
{
for (edge *ep = edges[p]; ep; ep = ep->next)
if (ep->v != par[p]) {
depth[ep->v] = depth[p] + 1;
par[ep->v] = p;
dfs(ep->v);
}
return ;
}
int get_diameter(void)
{
root = 1;
depth[root] = 1;
dfs(root);
for (int i = 1; i <= n; i++)
if (depth[i] > depth[root])
root = i;
// Calculating new depth with new root
memset(par, 0, sizeof(par));
memset(depth, 0, sizeof(depth));
depth[root] = 1;
dfs(root);
int p = root;
for (int i = 1; i <= n; i++)
if (depth[i] > depth[p])
p = i;
return depth[p];
}
} graph;
struct ed { int u, v, id;
ed(void) { u = v = id = 0; }
ed(int _1, int _2, int _3) {
u = min(_1, _2); v = max(_1, _2); id = _3; }
friend bool operator < (ed a, ed b) {
if (a.u == b.u) return a.v < b.v;
return a.u < b.u; }
} stk[maxn * 3];
int n;
int main(int argc, char** argv)
{
scanf("%d", &n);
int stop = 0;
for (int i = 1, a, b, c; i <= n - 2; i++) {
scanf("%d%d%d", &a, &b, &c);
stk[++stop] = ed(a, b, i);
stk[++stop] = ed(b, c, i);
stk[++stop] = ed(c, a, i);
}
sort(stk + 1, stk + stop + 1);
// Building graph to target
graph.n = n - 2;
for (int i = 2; i <= stop; i++)
if (stk[i].u == stk[i-1].u && stk[i].v == stk[i-1].v)
graph.add_edge(stk[i].id, stk[i-1].id);
// Getting diameter for graph
int res = graph.get_diameter();
printf("%d\n", res);
return 0;
}