Description
在 W 星球上有 \(n\) 个国家. 为了各自国家的经济发展, 他们决定在各个国家之间建设双向道路使得国家之间连通. 但是每个国家的国王都很吝啬, 他们只愿意修建恰好 \(n - 1\) 条双向道路. 每条道路的修建都要付出一定的费用, 这个费用等于道路长度乘以道路两端的国家个数之差的绝对值. 例如, 在下图中, 虚线所示道路两端分别有 \(2\) 个、\(4\) 个国家, 如果该道路长度为 \(1\), 则费用为 \(1 \times | 2 - 4 | = 2\). 图中圆圈里的数字表示 国家的编号.
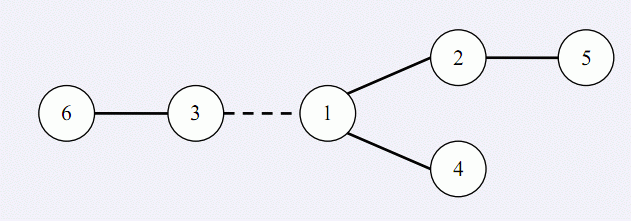
由于国家的数量十分庞大, 道路的建造方案有很多种, 同时每种方案的修建费用难以用人工 计算, 国王们决定找人设计一个软件, 对于给定的建造方案, 计算出所需要的费用. 请你 帮助国王们设计一个这样的软件.
Input
输入的第一行包含一个整数 \(n\), 表示 W 星球上的国家的数量, 国家从 \(1\) 到 \(n\) 编号. 接下来 \(n - 1\) 行描述道路建设情况, 其中第 \(i\) 行包含三个整数 \(a_i, b_i, c_i\), 表示第 \(i\) 条双向道路修建在 \(a_i\) 与 \(b_i\) 两个国家之间, 长度为 \(c_i\).
Output
输出一个整数, 表示修建所有道路所需要的总费用.
Sample Input
6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1Sample Output
20Data Range
对于所有数据, 满足:\(1 \leq a_i, b_i \leq n \leq 10^6, 0 \leq c_i \leq 10^6\)
Explanation
就是一个树形 DP, 但是在耒阳上交是可以直接用深搜的, 因为栈空间比较大.
但是本人作死决定写一个广搜, 结果发现在回溯那里卡壳了~ 然后花了半个多小时想了想, 最后手写了一个递归栈用来存储前一个状态的数据. 话说在 “眼睛+printf” 的时候还要考虑指针, 而且没了调试器我也就差不多完了因为 bug 出现在 printf 里......
总之多写一点手写递归还是有好处的~
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <queue>
#include <stack>
using namespace std;
typedef long long lli;
const int maxn = 1001000, maxm = 2001000;
class TreeDP
{
public:
struct edge
{
int u, v;
lli len;
edge *next;
};
int n, ecnt;
edge *edges[maxn], epool[maxm];
void add_edge(int u, int v, lli len)
{
edge *p = &epool[++ecnt],
*q = &epool[++ecnt];
p->u = u; p->v = v; p->len = len;
p->next = edges[u]; edges[u] = p;
q->u = v; q->v = u; q->len = len;
q->next = edges[v]; edges[v] = q;
return ;
}
int depth[maxn];
int size[maxn];
lli eval(void)
{
queue<int> que;
que.push(1);
depth[1] = 1;
while (!que.empty()) {
int p = que.front();
for (edge *ep = edges[p]; ep; ep = ep->next)
if (!depth[ep->v]) {
depth[ep->v] = depth[p] + 1;
que.push(ep->v);
}
que.pop();
}
// Calculating size
for (int i = 1; i <= n; i++)
size[i] = 1;
stack<pair<int, edge*> > stk;
stk.push(make_pair(1, edges[1]));
while (!stk.empty()) {
pair<int, edge*> pr = stk.top();
stk.pop();
int p = pr.first;
edge *ep = pr.second;
if (ep != NULL) {
stk.push(make_pair(p, ep->next));
if (depth[ep->v] == depth[p] + 1)
stk.push(make_pair(ep->v, edges[ep->v]));
} else {
if (!stk.empty()) {
size[stk.top().first] += size[p];
}
}
}
// Calculating total weight.
lli res = 0;
while (!que.empty())
que.pop();
que.push(1);
while (!que.empty()) {
int p = que.front();
for (edge *ep = edges[p]; ep; ep = ep->next)
if (depth[ep->v] == depth[p] + 1) {
res += ep->len * abs(size[ep->v] - (n - size[ep->v]));
que.push(ep->v);
}
que.pop();
}
return res;
}
} graph;
int n;
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int i = 1, a, b, c; i < n; i++) {
scanf("%d%d%d", &a, &b, &c);
graph.add_edge(a, b, c);
}
graph.n = n;
lli res = graph.eval();
printf("%lld\n", res);
return 0;
}