Description
新一届智能车大赛在 JL 大学开始啦! 比赛赛道可以看作是由 \(n\) 个矩形区域拼接而成 (如下图所示), 每个矩形的边都平行于坐标轴, 第 \(i\) 个矩形区域的左下角和右上角坐标分别为 \((x_{i,1},y_{i,1})\) 和 \((x_{i,2},y_{i,2})\).
题目保证:\(x_{i,1} \lt x_{i,2} = x_{i+1,1}\), 且 \(y_{i,1} \lt y_{i,2}\), 相邻两个 矩形一定有重叠在一起的边 (如图中虚线所示), 智能车可以通过这部分穿梭于矩形区域之间.
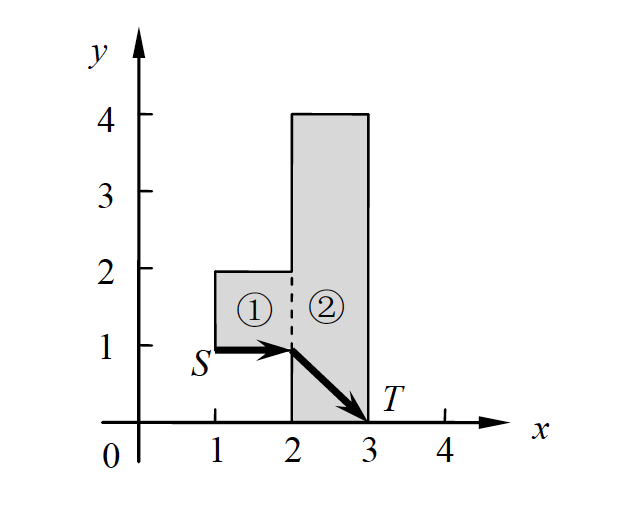
选手们需要在最快的时间内让自己设计的智能车从一个给定的起点 \(S\) 点到达一个给定的 终点 \(T\) 点, 且智能车不能跑出赛道. 假定智能车的速度恒为 \(v\) 且转向不消耗任何时间, 你能算出最快需要多少时间完成比赛么?
Input
输入的第一行包含一个正整数 \(n\), 表示组成赛道的矩形个数.
接下来 \(n\) 行描述这些矩形, 其中第 \(i\) 行包含 \(4\) 个整数 $x_ {i, 1}, y_ {i, 1}, x_ {i, 2}, y_ {i, 2}, 表示第 \(i\) 个矩形左下角和右上角坐标分别为 \((x_{i,1}, y_{i,1})\) 和 \((x_{i,2}, y_{i,2})\).
接下来一行包含两个整数 \(x_S, y_S\), 表示起点坐标.
接下来一行包含两个整数 \(x_T, y_T\), 表示终点坐标.
接下来一行包含一个实数 \(v\), 表示智能车的速度.
Output
仅输出一个实数, 至少精确到小数点后第六位, 为智能车完成比赛的最快时间. 对于每个 测试点, 如果你的输出结果和参考结果相差不超过 $10^ {-6}, 该测试点得满分, 否则不得分.
Sample Input
2
1 1 2 2
2 0 3 4
1 1
3 0
1.0Sample Output
2.41421356Data Range
\(N \leq 2000\), 所输入数字为绝对值小于 \(40000\) 的整数
Explanation
这道题是一道结论很水的结论题 (直接上计算几何无压力)
考虑直线最短, 那么如果不必要拐弯那就不拐, 所以拐点一定是赛道的边界定点, 一共有 \(2n\) 个边界, 所以 \(O(n^2)\) 暴力并不会超时~
上一个 double 就可以搞定精度问题, 然后就是类 SPFA 的最短路问题了
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define sqr(__x) ((__x)*(__x))
#define minimize(__x,__y) __x=min(__x,__y)
using namespace std;
typedef long long lli;
typedef double llf;
const int maxn = 8010;
const llf infinit = 1e99;
struct point { int x, y; };
int n, m, arr[10];
int x_1[maxn], y_1[maxn], x_2[maxn], y_2[maxn];
int sx, sy, tx, ty;
llf v, dist[maxn];
point p[maxn];
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d%d%d%d", &x_1[i], &y_1[i], &x_2[i], &y_2[i]);
scanf("%d%d%d%d", &sx, &sy, &tx, &ty);
if (sx > tx) // Of equal equivalence
swap(sx, tx), swap(sy, ty);
scanf("%lf", &v);
// Completed data input, preprocessing accessibility
p[m=1].x = sx, p[1].y = sy;
for (int i = 1; i < n; i++) {
// Special occasions, where we kick out the useless
if (sx > x_2[i]) continue;
if (x_2[i] > tx) break;
arr[1] = y_1[i], arr[2] = y_2[i];
arr[3] = y_1[i+1], arr[4] = y_2[i+1];
sort(arr + 1, arr + 1 + 4);
// Create abstract points with potential turns
p[++m].x = x_2[i], p[m].y = arr[2];
p[++m].x = x_2[i], p[m].y = arr[3];
}
p[++m].x = tx, p[m].y = ty;
// Relaxing distances.
for (int i = 2; i <= m; i++)
dist[i] = infinit;
for (int i = 1; i < m; i++) {
llf ax = (llf)p[i].x * 1.0, ay = (llf)p[i].y * 1.0;
llf maxx = infinit, minn = -infinit;
for (int j = i + 1; j <= m; j++) {
llf bx = (llf)p[j].x * 1.0, by = (llf)p[j].y * 1.0;
llf len = 0.0;
if (bx == ax) {
len = abs(by - ay);
minimize(dist[j], dist[i] + len);
continue;
} // Avoid SIGFPE errors
llf slope = (by - ay) / (bx - ax);
if (slope <= maxx && slope >= minn) {
len = sqrt(sqr(by - ay) + sqr(bx - ax));
minimize(dist[j], dist[i] + len);
} // If is an accessible point
if (j % 2 == 0) minn = max(minn, slope);
else maxx = min(maxx, slope);
}
}
// Output time, as distance divided by velocity
llf res = dist[m] / v;
printf("%.8lf\n", res);
return 0;
}