Description
度量一个有向图联通情况的一个指标时连通数, 指图中可达顶点对的个数.
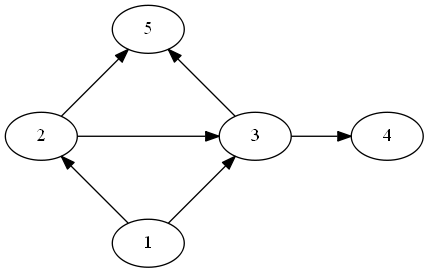
在上图中, 顶点 \(1\) 可以到达 \(1, 2, 3, 4, 5\);
顶点 \(2\) 可以到达 \(2, 3, 4, 5\);
顶点 \(3\) 可以到达 \(3, 4, 5\);
顶点 \(4, 5\) 均只能到达自身, 所以它的连通数为 \(14\);
Input
输入数据第一行是图顶点的数量, 一个正整数 \(n\).
接下来 \(n\) 行, 每行 \(n\) 个字符. 第 \(i\) 行第 \(j\) 列的 \(1\) 表示顶点 \(i\) 到 \(j\) 有边,\(0\) 则表示无边.
Output
输出一行一个整数, 表示该图的连通数.
Sample Input
3
010
001
100Sample Output
9Data Range
对于 100% 的数据,\(n \leq 2000\).
Explanation
输入需要字符串给差评......
题干偷懒只放图差评...... 害得我写题解还得把题干重新抄一遍......
预先处理强连通分量缩点, 然后缩出来的图就一定是一个 DAG 了. 这时用一些奇特的技巧 在这个 DAG 上面瞎搞打标记, 最后可以得到值.
感觉这个和某一年 NOIP 里面的题目很相似啊......
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <stack>
#include <bitset>
#include <cstring>
using namespace std;
typedef long long lli;
const int maxn = 4010, maxm = 4000100;
class Graph
{
public:
struct edge
{
int u, v;
edge *next;
};
};
class Tarjan : public Graph
{
public:
int n, ecnt, dcnt, bcnt;
edge *edges[maxn], epool[maxm];
void add_edge(int u, int v)
{
edge *p = &epool[++ecnt];
p->u = u; p->v = v;
p->next = edges[u]; edges[u] = p;
return ;
}
int dfn[maxn], low[maxn], instk[maxn];
int belong[maxn], bsize[maxn];
stack<int> stk;
void dfs(int p)
{
dfn[p] = low[p] = ++dcnt;
stk.push(p);
instk[p] = true;
for (edge *ep = edges[p]; ep; ep = ep->next) {
int q = ep->v;
if (!dfn[q]) {
dfs(q);
if (low[q] < low[p])
low[p] = low[q];
} else if (instk[q] && dfn[q] < low[p])
low[p] = dfn[q];
}
if (dfn[p] == low[p]) {
bcnt += 1;
bsize[bcnt] = 0;
int q = 0;
do {
q = stk.top();
stk.pop();
instk[q] = false;
belong[q] = bcnt;
bsize[bcnt] += 1;
} while (q != p);
}
return ;
}
void init(int n)
{
this->n = n;
return ;
}
void eval(void)
{
bcnt = dcnt = 0;
while (!stk.empty())
stk.pop();
memset(instk, 0, sizeof(instk));
memset(dfn, 0, sizeof(dfn));
memset(low, 0, sizeof(low));
memset(belong, 0, sizeof(belong));
for (int i = 1; i <= n; i++)
if (!dfn[i])
dfs(i);
return ;
}
} graph;
class TreeDP : public Graph
{
public:
int n, ecnt;
int in_degree[maxn];
edge *edges[maxn], epool[maxm];
void add_edge(int u, int v)
{
edge *p = &epool[++ecnt];
p->u = u; p->v = v;
p->next = edges[u]; edges[u] = p;
in_degree[v] += 1;
return ;
}
void init(int n)
{
this->n = n;
for (int i = 1; i <= n; i++)
for (edge *ep = graph.edges[i]; ep; ep = ep->next)
if (graph.belong[i] != graph.belong[ep->v])
this->add_edge(graph.belong[ep->v], graph.belong[i]);
return ;
}
// Now we are using some magic STL templates to ease the code.
bitset<maxn> mark[maxn];
int eval(void)
{
stack<int> stk;
for (int i = 1; i <= graph.bcnt; i++)
mark[i].reset();
for (int i = 1; i <= n; i++)
mark[graph.belong[i]][i] = true;
// Pushing stuff into the stack
for (int i = 1; i <= graph.bcnt; i++)
if (in_degree[i] <= 0)
stk.push(i);
// Evaluating
while (!stk.empty()) {
int cur = stk.top();
stk.pop();
for (edge *ep = edges[cur]; ep; ep = ep->next) {
mark[ep->v] |= mark[cur];
in_degree[ep->v] -= 1;
if (!in_degree[ep->v])
stk.push(ep->v);
}
}
// Getting result
int res = 0;
for (int i = 1; i <= graph.bcnt; i++)
for (int j = 1; j <= n; j++)
if (mark[i][j])
res += graph.bsize[i];
return res;
}
} tree;
int n;
char str[maxn];
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", str + 1);
for (int j = 1; j <= n; j++)
if (str[j] == '1')
graph.add_edge(i, j);
}
graph.init(n);
// Resolving graph for SCCs with Tarjan
graph.eval();
// Building tree structure with preresolved data upstream from Tarjan
tree.init(n);
// Retrieving result
int res = tree.eval();
printf("%d\n", res);
return 0;
}