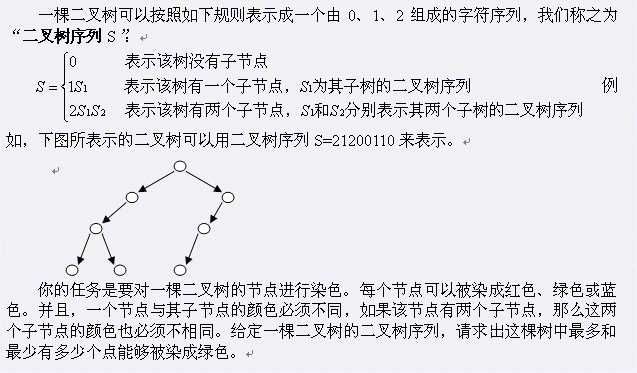
Description
Input
仅有一行, 不超过 \(500000\) 个字符, 表示一个二叉树序列.
Output
输出文件也只有一行, 包含两个数, 依次表示最多和最少有多少个点能够被染成绿色.
Sample Input
1122002010Sample Output
5 2Explanation
先用递归把树的结构求出来 (这个应该不用说了吧~)
然后考虑每层 (每个节点) 涂哪种颜色 (RGB), 再记一下子树上涂的绿节点最多和最少的 情况下绿节点一共涂了多少个节点.
最后在根节点 (无根树, 随便选一个根节点) 看一下三种颜色哪个更划算一点就可以稳稳输出了.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#define min_3(__x,__y,__z) min(min(__x,__y),__z)
#define max_3(__x,__y,__z) max(max(__x,__y),__z)
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
#define range(_begin,_end) rep(_,_begin,_end)
#define range_(_begin,_end) rep(__,_begin,_end)
using namespace std;
typedef long long lli;
const int maxn = 500100;
class TreeDP
{
public:
int ch[maxn][2], par[maxn];
int root, ncnt;
int dp[maxn][3][2];
int make_node(void)
{
int p = ++ncnt;
ch[p][0] = ch[p][1] = par[p] = 0;
return p;
}
int build_tree(int& pos, char str[])
{
int cnt = str[pos] - '0';
int p = make_node();
if (cnt >= 1) { pos++;
ch[p][0] = build_tree(pos, str);
par[ch[p][0]] = p;
} if (cnt >= 2) { pos++;
ch[p][1] = build_tree(pos, str);
par[ch[p][1]] = p;
}
return p;
}
void build_tree(char str[])
{
int pos = 0;
root = build_tree(pos, str);
return ;
}
void dfs(int p)
{
if (!ch[p][0]) { // No children
dp[p][0][0] = 0; dp[p][0][1] = 0;
dp[p][1][0] = dp[p][1][1] = 1;
dp[p][2][0] = 0; dp[p][2][1] = 0;
} else if (!ch[p][1]) { // One child
dfs(ch[p][0]);
dp[p][0][0] = min( dp[ ch[p][0] ][1][0], dp[ ch[p][0] ][2][0] );
dp[p][0][1] = max( dp[ ch[p][0] ][1][1], dp[ ch[p][0] ][2][1] );
dp[p][1][0] = min( dp[ ch[p][0] ][2][0], dp[ ch[p][0] ][0][0] ) + 1;
dp[p][1][1] = max( dp[ ch[p][0] ][2][1], dp[ ch[p][0] ][0][1] ) + 1;
dp[p][2][0] = min( dp[ ch[p][0] ][0][0], dp[ ch[p][0] ][1][0] );
dp[p][2][1] = max( dp[ ch[p][0] ][0][1], dp[ ch[p][0] ][1][1] );
} else { // Two children
dfs(ch[p][0]); dfs(ch[p][1]);
dp[p][0][0] = min( dp[ ch[p][0] ][1][0] + dp[ ch[p][1] ][2][0], dp[ ch[p][0] ][2][0] + dp[ ch[p][1] ][1][0]);
dp[p][0][1] = max( dp[ ch[p][0] ][1][1] + dp[ ch[p][1] ][2][1], dp[ ch[p][0] ][2][1] + dp[ ch[p][1] ][1][1]);
dp[p][1][0] = min( dp[ ch[p][0] ][2][0] + dp[ ch[p][1] ][0][0], dp[ ch[p][0] ][0][0] + dp[ ch[p][1] ][2][0]) + 1;
dp[p][1][1] = max( dp[ ch[p][0] ][2][1] + dp[ ch[p][1] ][0][1], dp[ ch[p][0] ][0][1] + dp[ ch[p][1] ][2][1]) + 1;
dp[p][2][0] = min( dp[ ch[p][0] ][0][0] + dp[ ch[p][1] ][1][0], dp[ ch[p][0] ][1][0] + dp[ ch[p][1] ][0][0]);
dp[p][2][1] = max( dp[ ch[p][0] ][0][1] + dp[ ch[p][1] ][1][1], dp[ ch[p][0] ][1][1] + dp[ ch[p][1] ][0][1]);
}
// printf("dfs %d par %d ch %d, %d\n", p, par[p], ch[p][0], ch[p][1]);
// printf(" RED [ %d %d ] GREEN [ %d %d ] BLUE [ %d %d ]\n", dp[p][0][0], dp[p][0][1], dp[p][1][0], dp[p][1][1], dp[p][2][0], dp[p][2][1]);
return ;
}
int min_res, max_res;
void eval(void)
{
dfs(1);
min_res = min_3( dp[1][0][0], dp[1][1][0], dp[1][2][0] );
max_res = max_3( dp[1][0][1], dp[1][1][1], dp[1][2][1] );
return ;
}
} graph;
char str[maxn];
int main(int argc, char** argv)
{
scanf("%s", str);
graph.build_tree(str);
graph.eval();
printf("%d %d\n", graph.max_res, graph.min_res);
return 0;
}