Description
lxhgww 最近接到了一个生成字符串的任务, 任务需要他把 \(n\) 个 \(1\) 和 \(m\) 个 \(0\) 组成 字符串, 但是任务还要求在组成的字符串中, 在任意的前 \(k\) 个字符中,\(1\) 的个数不能少于 \(0\) 的个数. 现在 lxhgww 想要知道满足要求的字符串共有多少个, 聪明的程序员们, 你们能帮助他吗?
Input
输入数据是一行, 包括 \(2\) 个数字 \(n\) 和 \(m\).
Output
输出数据是一行, 包括 \(1\) 个数字, 表示满足要求的字符串数目, 这个数可能会很大, 只需 输出这个数除以 \(20100403\) 的余数.
Sample Input
2 2Sample Output
2Data Range
对于 30% 的数据, 保证 \(1 \leq m \leq n \leq 1000\) 对于 100% 的数据, 保证 \(1 \leq m \leq n \leq 1000000\)
Explanation
最开始想的是 \(O(mn)\) 的动规转移方程, 然后果断发现会 T
后来发现可以转化成一个在矩阵上转移的问题, 然后就开始想应该这道题不会有什么一些 玄学的 \(O(m \log n)\) 或 \(O(n \log m)\) 的做法, 想了一阵就忘了有这道题了...... 233
今天突然拿出来, 打算看一下题解, 发现我只想了一个头, 然后膜完了题解发现居然是一道 排列组合题...... 我数学学得不好 QAQ
但是题解还是理解了的~
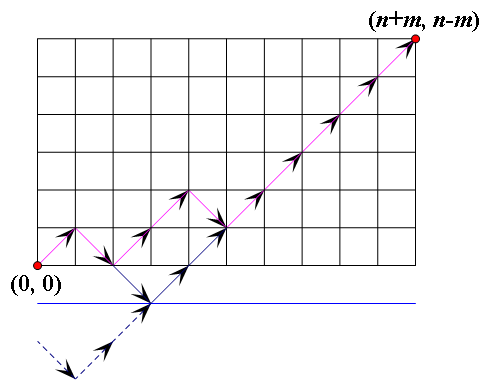
设 \(1\) 为向 \((1,1)\) 方向走,\(0\) 为向 \((1,-1)\) 方向走. 那么题意可转化为从 \((0,0)\) 走到 \((n+m,n-m)\) 且不能跨过 \(y = 0\) 的方案数. 总方案数 \(C_{n+m}^{n}\), 然后要减去不合法的即线路通过 \(y = -1\) 的. 将线路与 \(y = -1\) 交点的左边沿着 \(y = -1\) 做对称操作, 则最后等价于从 \((0,-2)\) 走到 \((n+m,n-m)\) 的方案数. 因为从 \((0,-2)\) 走到 \((n+m,n-m)\) 需要向上走 \(n-m+2\) 次, 一共要走 \(n+m\) 次. 设向上向下各走 \(x,y\), 那么 \(x+y=n+m, x-y=n-m+2\) 得到 \(x=n+1,y=m-1\), 所以不合法的方案为 \(C_{n+m}^{m-1}\).
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
typedef long long lli;
typedef lli i64;
const int modr = 20100403;
lli extended_euclid(lli a, lli b, lli& x, lli& y)
{
if (b == 0) {
x = 1; y = 0;
return a;
}
lli tmp = extended_euclid(b, a % b, x, y);
lli t = x; x = y;
y = t - a / b * y;
return tmp;
}
lli reverse(lli a)
{
// Equivalent division results under mod modr for 1 / a
lli x, y;
extended_euclid(a, modr, x, y);
return (x % modr + modr) % modr;
}
lli factorial(lli a)
{
lli res = 1;
for (int i = 1; i <= a; i++)
res = res * i % modr;
return res;
}
lli combinations(lli a, lli b)
{
lli x = factorial(a),
y = factorial(b),
z = factorial(a - b);
return x * reverse(y) % modr * reverse(z) % modr;
}
lli n, m;
int main(int argc, char** argv)
{
scanf("%lld%lld", &n, &m);
lli res = combinations(n + m, n) - combinations(n + m, n + 1);
res = (res % modr + modr) % modr;
printf("%lld\n", res);
return 0;
}