Description
画一个等边三角形, 把三边的中点连接起来, 得到四个三角形, 把它们称为 T1, T2, T3, T4, 如图 1. 把前三个三角形也这样划分, 得到 12 个更小的三角形: T11, T12, T13, T14, T21, T22, T23, T24, T31, T32, T33, T34, 如图 2. 把编号以 1, 2, 3 结尾的三角形又继续划分...... 最后得到的分形称为 Sierpinski 三角形.
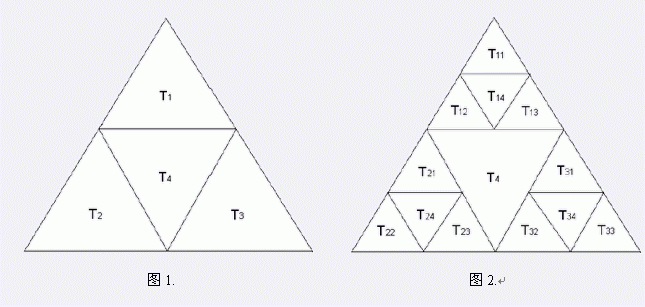
图 2. 如果 B 不包含 A, 且 A 的某一条完整的边是 B 的某条边的一部分, 则我们说 A 靠在 B 的边上. 例如 T12 靠在 T24 和 T4 上, 但不靠在 T32 上. 给出 Spierpinski 三角形中的一个三角形, 找出它靠着的所有三角形.
Input
输入仅一行, 即三角形的编号, 以 T 开头, 后面有 n 个 1 到 4 的数字. 仅最后一个数字可能为 4.
Output
输出每行一个三角形编号, 按字典序从小到大排列.
Sample Input
T312Sample Output
T314
T34
T4Data Range
50% 的数据满足:\(1 \leq n \leq 5\)
100% 的数据满足:\(1 \leq n \leq 50\)
Solution
我们可以发现这一点: 题中所给的三角形一定是所有划分出来的三角形中的最小的一个之一. 所以不会有比这个三角形还小的三角形. 另外由于边都是顶点对顶点, 不会胡乱切出来 (其实 我也不知道我刚才说了些什么, 不要管了), 所以这一个三角形的每一条边最多只会与一个 三角形相邻 (也就是说, 总共最多有三个三角形相邻).
进一步地, 编号为 1, 2, 3 的三角形不会互相相邻, 如果他们的大小相同且为同一个更大一点 的三角形拆分出来的三角形. 他们只会和相邻的编号为 4 的三角形相邻.
大概这样推断一下, 就会发现把 \(i\) 从 \(n\) 开始扫到 \(1\) 就可以了, 然后中间经过的三角形一定最多只有 \(3\) 个, 然后还是按字典序排布的, 就不用最后比较一下再输出了
然后就这样 1A 了 233~
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long lli;
const int maxn = 60;
void print_triangle(int dat[]) {
if (dat[0] <= 0) return ; printf("T");
for (int i = 1; i <= dat[0]; i++) printf("%d", dat[i]);
printf("\n"); return ; }
int n, arr[maxn];
int tri[4][maxn]; // Guranteed at most 3 of them being used
char str[maxn];
int main(int argc, char** argv)
{
scanf("%s", str);
n = strlen(str) - 1;
for (int i = 1; i <= n; i++)
tri[1][i] = tri[2][i] = tri[3][i] = arr[i] = str[i] - '0';
// Exceptions, only once
if (arr[n] == 4) {
for (int i = 1; i <= 3; i++) {
tri[i][0] = n;
tri[i][n] = i;
print_triangle(tri[i]);
}
return 0;
}
// Initial states of TRI[0]'s adjacency to sides in current triangle
bool left = true,
right = true,
bottom = true;
// The count of triangles, if reached 3 then exit
int tcnt = 0;
// Processing from nearest to farthest
for (int i = n; i >= 1; i--) {
int pos = arr[i];
// Current set position... triangle always 4.
if ((pos == 1 && bottom)
|| (pos == 2 && right)
|| (pos == 3 && left)) {
tcnt++;
tri[tcnt][0] = i;
tri[tcnt][i] = 4;
}
// Set adjacency
if (pos == 1)
bottom = false;
else if (pos == 2)
right = false;
else if (pos == 3)
left = false;
}
for (int i = 1; i <= tcnt; i++)
print_triangle(tri[i]);
return 0;
}