Description
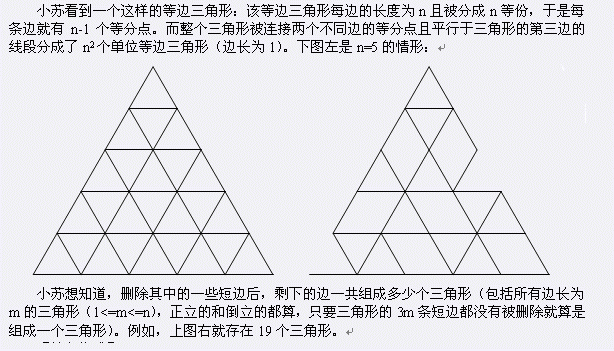
Input
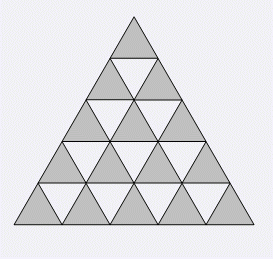
大三角形的所有短边可以看成由 \(\frac{n \cdot (n+1)}{2}\) 个单位三角形的边界组成. 如下图的灰色三角形所示. 其中第 \(1\) 排有 \(1\) 个灰色三角形, 第 \(2\) 排有 \(2\) 个灰色三角形,. ...... , 第 \(n\) 排有 \(n\) 个灰色三角形. 所以输入格式是这样规定的: 输入 第一行为正整数 \(n\), 其中 \(1 \leq n \leq 1000\), 表示大三角形每边的长度. 接下来的 \(n\) 行, 第 \(i+1\) 行有 \(i\) 组数, 从左到右每组数描述一个三角形, 每组数都有 \(3\) 个数, 这 \(3\) 个数非 \(0\) 即 \(1\), 表示对应的短边是否被删除,\(0\) 表示已被删除,\(1\) 表示未被删除, 依次按照三角形的左、右、下边的顺序来描述. 所以第 \(i+1\) 行有 \(3i\) 个数, 每个数是 \(0\) 或 \(1\)
Output
仅包含一个整数 \(T\), 表示有多少个三角形的边界都没有被删除.
Sample Input
5
1 1 1
1 1 0 1 1 0
1 1 1 1 1 1 1 0 1
1 0 1 1 1 1 0 1 1 1 1 1
0 1 1 1 1 1 0 1 1 1 1 1 0 1 1Sample Output
19Explanation
用前缀和来维护区间查询连续性.
然后直接上暴力就可以解出此题. 虽然 \(O(n^3)\) 看起来会爆, 但是考虑到各种剪枝和 优化再加上 bzoj 宽裕大方的 10s 时限, 其实是可以过掉的.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
using namespace std;
typedef long long lli;
const int maxn = 1010;
class line
{
public:
int arr[maxn], n;
void add(int pos, int val) {
arr[pos] += val;
return ; }
void build(void) {
for (int i = 2; i <= n; i++)
arr[i] += arr[i - 1];
return ; }
bool check(int l, int r) {
return arr[r] - arr[l - 1] == r - l + 1; }
};
line tlef[maxn], trig[maxn]; // Triangle left, right.
bool low[maxn][maxn];
int n;
bool check_upright_triangle(int row, int l, int r)
{
int len = r - l + 1;
return tlef[l].check(row-l+1 - len + 1, row-l+1)
&& trig[row-r+1].check(r - len + 1, r);
}
bool check_inverted_triangle(int row, int l, int r)
{
int len = r - l + 1;
return trig[row-l+2].check(l, l+len-1)
&& tlef[r+1].check(row-r+1, row-r+1 + len - 1);
}
int main(int argc, char** argv)
{
scanf("%d", &n);
rep(i, 1, n) tlef[i].n = trig[i].n = n - i + 1;
rep(i, 1, n) rep(j, 1, i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (x) tlef[j].add(i-j+1, 1);
if (y) trig[i-j+1].add(j, 1);
low[i][j] = z;
}
rep(i, 1, n)
tlef[i].build(),
trig[i].build();
// Processing with brute force, only a bit faster.
int res = 0;
// i is the row number #i
for (int i = 1; i <= n; i++) {
// l, r represents the left bound and the right bound of the triangle
int l = 1, r = 0;
for (int j = 1; j <= i; j++) {
// Impossible detection. Does not form a triangle anymore.
if (low[i][j]) r += 1;
else l = j+1, r = j;
// Choosing r as right bound, k as left bound of detecting triangle
for (int k = l; k <= r; k++) {
res += check_upright_triangle(i, k, r);
// if it satisfies the inverted triangle.
if (r-k+1 <= n-i)
res += check_inverted_triangle(i, k, r);
}
}
}
// Output result.
printf("%d\n", res);
return 0;
}