Description
Input
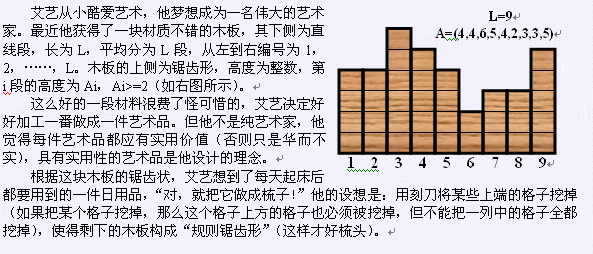
第一行为整数 \(L\), 其中 \(4 \leq L \leq 100000\), 且有 50% 的数据满足 \(L \leq 10^4\), 表示木板下侧直线段的长. 第二行为 \(L\) 个正整数 \(A_1, A_2, \ldots, A_L\).
Output
仅包含一个整数 \(D\), 表示为使梳子面积最大, 需要从木板上挖掉的格子数.
Sample Input
9
4 4 6 5 4 2 3 3 5Sample Output
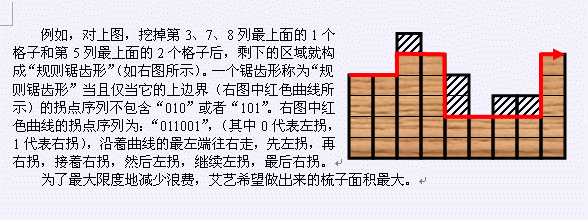
3Explanation
贪心, 此题有一些结论...... 比如强行在某一些地方挖一个洞可以变得更好等等......
当然此题的关键点在于, 不会出现长度至少为 \(3\) 的单调序列.
然后参照以下题解:Solution for bzoj1200, Microsoft Word
证明根本看不懂~
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define minimize(__x,__y) __x=min(__x,__y)
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
#define range(_begin,_end) rep(_,_begin,_end)
using namespace std;
typedef long long lli;
const int maxn = 100100;
const lli infinit = 0x007f7f7f7f7f7f7fll;
int n;
int a[maxn], b_arr[maxn][5][3];
lli dp_arr[maxn][5][3][2];
#define b(_a,_b,_c) b_arr[_a][(_b)+2][(_c)+1]
#define dp(_a,_b,_c,_d) dp_arr[_a][(_b)+2][(_c)+1][(_d)]
int main(int argc, char** argv)
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
// Setting initial status
memset(dp_arr, 122, sizeof(dp_arr));
rep(j, 0, 2) if (j+1 <= n) rep(k, -1, 1)
if (a[j + 1] + k <= a[1]) {
b(1, j, k) = a[j + 1] + k;
range(0,1) dp(1, j, k, _) = a[1] - b(1, j, k);
}
// Dynamic programming.
rep(i, 2, n) rep(j, -2, 2) if (i+j <= n && i+j > 0)
rep(k, -1, 1) if (a[i+j] + k <= a[i]) {
b(i, j, k) = a[i+j] + k;
int tmp = a[i] - b(i, j, k);
// Updating current status
rep(j1, -2, 2) rep(k1, -1, 1) {
if (b(i - 1, j1, k1) > b(i, j, k))
minimize(dp(i, j, k, 0), dp(i - 1, j1, k1, 1) + tmp);
else if (b(i - 1, j1, k1) < b(i, j, k))
minimize(dp(i, j, k, 1), dp(i - 1, j1, k1, 0) + tmp);
else range(0,1)
minimize(dp(i, j, k, _), dp(i - 1, j1, k1, _) + tmp);
}
}
// Retrieve results
lli res = infinit;
rep(j, -2, 2) rep(k, -1, 1) {
minimize(res, dp(n, j, k, 0));
minimize(res, dp(n, j, k, 1));
}
printf("%lld\n", res);
return 0;
}