| Problem Specification | Value |
|---|---|
| Time Limit | 15 Sec |
| Memory Limit | 162 MB |
| Submit | 2546 |
| Solved | 1064 |
Description
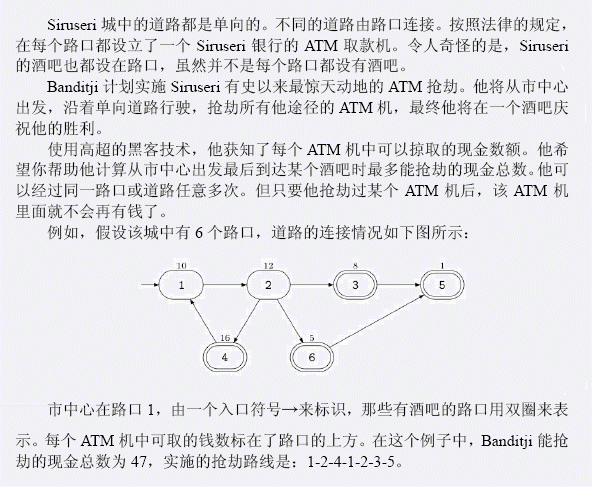
Input
第一行包含两个整数 N、M. N 表示路口的个数, M 表示道路条数. 接下来 M 行, 每行两个整数, 这两个整数都在 1 到 N 之间, 第 i+1 行的两个整数表示第 i 条道路的起点和终点的路口编号. 接下来 N 行, 每行一个整数, 按顺序表示每个路口处的 ATM 机中的钱数. 接下来一行包含两个整数 S、P, S 表示市中心的编号, 也就是出发的路口. P 表示酒吧数目. 接下来的一行中有 P 个整数, 表示 P 个有酒吧的路口的编号
Output
输出一个整数, 表示 Banditji 从市中心开始到某个酒吧结束所能抢劫的最多的现金总数.
Sample Input
6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1 5
1 4
4
3
5
6Sample Output
47HINT
50% 的输入保证 N, M<=3000. 所有的输入保证 N, M<=500000. 每个 ATM 机中可取的钱数为一个非负整数且不超过 4000. 输入数据保证你可以从市中心沿着 Siruseri 的单向的道路到达其中的至少一个酒吧.
Explanation
先强连通分量缩点, 得到一个有向无环图.
然后简单跑一遍 SPFA 就可以了.
很容易 WA~ 并且不停 Presentation Error 233~
Example Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <stack>
#include <queue>
#include <cstring>
using namespace std;
typedef long long lli;
const int maxn = 500100, maxm = 500100;
const lli infinit = 0x007f7f7f7f7f7f7fll;
class Graph
{
public:
struct edge
{
int u, v;
edge *next;
};
edge *edges[maxn], epool[maxm];
int n, ecnt;
void addedge(int u, int v)
{
edge *p = &epool[++ecnt];
p->u = u; p->v = v;
p->next = edges[u]; edges[u] = p;
return ;
}
void clear(void)
{
memset(edges, 0, sizeof(edges));
memset(epool, 0, sizeof(epool));
n = ecnt = 0;
return ;
}
};
class Tarjan : public Graph
{
public:
int dfn[maxn], low[maxn];
int belong[maxn]; // This is the result of the final procedure...
int bcnt, dcnt;
stack<int> stk;
bool instk[maxn];
// My greatest gratitude to @byvoid for this article...
// https://www.byvoid.com/blog/scc-tarjan
void dfs(int p)
{
dfn[p] = low[p] = ++dcnt; // Assign DFS number index
stk.push(p);
instk[p] = true;
for (edge *ep = edges[p]; ep; ep = ep->next) {
int q = ep->v;
if (!dfn[q]) {
dfs(q);
if (low[p] > low[q])
low[p] = low[q];
} else if (instk[q] && dfn[q] < low[p])
low[p] = dfn[q];
}
if (dfn[p] == low[p]) {
bcnt++; // Assign new belong / block counter / index
int q = 0;
do {
q = stk.top();
stk.pop();
instk[q] = false;
belong[q] = bcnt;
} while (q != p);
}
return ;
}
void eval(void)
{
while (!stk.empty())
stk.pop();
bcnt = dcnt = 0;
memset(dfn, 0, sizeof(dfn));
memset(low, 0, sizeof(low));
for (int i = 1; i <= n; i++)
if (!dfn[i])
dfs(i);
return ;
}
} graph;
class SPFA : public Graph
{
public:
lli dist[maxn];
lli weight[maxn];
bool inque[maxn];
int s;
void eval(void)
{
queue<int> que;
for (int i = 1; i <= n; i++)
inque[i] = false, dist[i] = infinit;
que.push(s);
inque[s] = true;
dist[s] = weight[s];
while (!que.empty()) {
int p = que.front();
que.pop();
for (edge *ep = edges[p]; ep; ep = ep->next) {
if (dist[p] + weight[ep->v] > dist[ep->v] || dist[ep->v] >= infinit) {
dist[ep->v] = dist[p] + weight[ep->v];
if (!inque[ep->v]) {
que.push(ep->v);
inque[ep->v] = true;
}
}
}
inque[p] = false;
}
return ;
}
} spfa;
int n, m, S, P;
int v[maxn];
int pub[maxn], pubcnt;
int main(int argc, char** argv)
{
scanf("%d%d", &n, &m);
graph.n = n;
spfa.n = n;
for (int i = 1, a, b; i <= m; i++) {
scanf("%d%d", &a, &b);
graph.addedge(a, b);
}
for (int i = 1; i <= n; i++)
scanf("%d", &v[i]);
scanf("%d%d", &S, &P);
for (int i = 1, a; i <= P; i++) {
scanf("%d", &a);
pub[++pubcnt] = a;
}
// Done input (That was a lot of input!)
graph.eval();
// Done evaluating graph values, now building new graph for SPFA.
for (int i = 1; i <= m; i++) {
Graph::edge* ed = &graph.epool[i];
int p = graph.belong[ed->u],
q = graph.belong[ed->v];
if (p != q)
spfa.addedge(p, q);
}
for (int i = 1; i <= n; i++)
spfa.weight[graph.belong[i]] += v[i];
spfa.s = graph.belong[S];
spfa.eval();
lli res = 0;
for (int i = 1; i <= pubcnt; i++) {
if (spfa.dist[graph.belong[pub[i]]] < infinit)
res = max(res, spfa.dist[graph.belong[pub[i]]]);
}
printf("%lld", res);
return 0;
}