Description
你准备给弟弟 Ike 买一件礼物, 但是, Ike 挑选礼物的方式很特别: 他只喜欢那些能按照他 1 特有方式排成有序的东西.
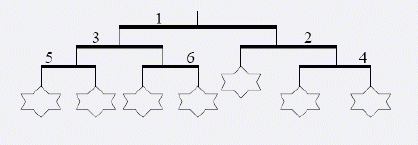
你准备给 Ike 买一个风铃. 风铃是一种多层的装饰品, 一般挂在天花板上. 每个风铃都包含一些由竖直的线连起来的水平杆. 每根杆的两端都有线连接, 下面或者挂着另一根水平杆, 或者挂着一个玩具. 下面是一个风铃的例子:
为使你的弟弟满意, 你需要选一个满足下面两个条件的风铃:
- 所有的玩具都在同一层 (也就是说, 每个玩具到天花板之间的杆的个数是一样的) 或至多相差一层.
- 对于两个相差一层的玩具, 左边的玩具比右边的玩具要更靠下一点.
风铃可以按照下面的规则重新排列: 任选一根杆, 将杆两端的线 “交换”. 也就是解开一根杆左右两端的线, 然后将它们分别绑到杆的另一端. 注意这个操作不会改变下面的杆上线的排列顺序.
由于你正在参加信息学奥林匹克的训练, 所以你决定设计一个算法, 判断能否通过重新排列, 将一个给定的风铃变为 Ike 喜欢的样子.
考虑上面的例子, 上图中的风铃满足条件 \(1\), 却不满足条件 \(2\)----最左边的那个玩具比它右边的要高.
但是, 我们可以通过下面的步骤把这个风铃变成一个 Ike 喜欢的形式:
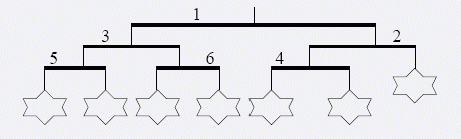
- 第一步, 将杆 \(1\) 的左右两端交换, 这使得杆 \(2\) 和杆 \(3\) 的位置互换, 交换的结果如下图所示:
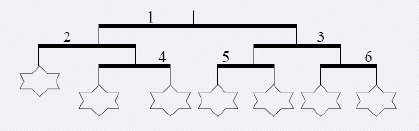
- 第二步, 也是最后一步, 将杆 \(2\) 的左右两端交换, 这使得杆 \(4\) 到了左边, 原来在左边的玩具到了右边, 交换的结果如下图所示:

现在这个风铃就满足 Ike 的条件了.
你的任务是: 给定一个风铃的描述, 求出最少需要多少次交换才能使这个风铃满足 Ike 的条件 (如果可能的话).
Input
输入的第一行包含一个整数 \(n (1 \leq n \leq 100000)\), 表示风铃中有多少根杆.
接下来的 \(n\) 行描述杆的连接信息. 这部分的第 \(i\) 行包含两个由空格分割的整数 \(l_i, r_i\), 描述杆 \(i\) 的左右两端悬挂的东西. 如果挂的是一个玩具, 则对应的值为 \(-1\), 否则为挂在下面的杆的编号.
如果杆 \(i\) 下面挂有其它杆, 则这些杆的编号将严格大于 \(i\). 杆 \(1\) 位于风铃的顶部.
Output
输出仅包含一个整数. 表示最少需要多少次交换能使风铃满足 Ike 的条件. 如果不可能满足, 输出 \(-1\).
Sample Input
6
2 3
-1 4
5 6
-1 -1
-1 -1
-1 -1Sample Output
2Explanation
因为只能交换相邻两棵子树, 所以如果有一根杆 (其实就是一个节点) 的两个子树之间深度差超过 \(2\), 那么无论怎么换都不会使这个深度减小.
所以如果树的最大深度与最小深度值差超过 \(2\), 直接返回无解.
如果所有叶子结点的深度都一样的话, 不需要做任何交换.
接下来如果有一个节点左右两个子树均同时包含最小深度和最大深度, 也是无法通过交换使得这棵树 “平衡” 的; 否则需要进行一次交换.
大概按照这个思路 dfs 一发即可......
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <queue>
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
#define range(_begin,_end) rep(_,_begin,_end)
using namespace std;
typedef long long lli;
const int maxn = 200100;
const int infinit = 0x3f3f3f3f;
class TreeDP
{
public:
#define lc(_p) ch[_p][0]
#define rc(_p) ch[_p][1]
int n, root, max_dep, min_dep;
int ch[maxn][2], par[maxn];
int depth[maxn];
void set_child(int parent, int child, int side)
{
par[child] = parent;
ch[parent][side] = child;
return ;
}
int final_res;
int dfs(int p, int depth)
{
// Returns a bit-compressed data
// 2 if has minimum depth, 1 if has maximum depth
// The two bits are combined with logic or.
// printf("dfs %d %d\n", p, depth);
if (p == 0) {
if (depth == max_dep)
return 1;
else if (depth == min_dep)
return 2;
}
// Setting to check both children
int lv = dfs(lc(p), depth + 1),
rv = dfs(rc(p), depth + 1);
// If they all have differential heights, then it is certain that we
// cannot swap sticks to make things right.
// THINK ABOUT IT.
if (lv == 3 && rv == 3) {
final_res = -infinit;
return -1;
}
// Adding some data.
if (lv == 2 && (rv == 1 || rv == 3))
final_res += 1;
else if (lv == 3 && rv == 1)
final_res += 1;
return lv | rv;
}
int eval(void)
{
// Getting maximum depth and minimum depth
max_dep = 0, min_dep = infinit;
queue<int> que;
que.push(root);
depth[root] = 1;
while (!que.empty()) {
int p = que.front();
que.pop();
range(0, 1) if (!ch[p][_]) {
max_dep = max(max_dep, depth[p] + 1);
min_dep = min(min_dep, depth[p] + 1);
}
range(0, 1) if (ch[p][_]) {
depth[ch[p][_]] = depth[p] + 1;
que.push(ch[p][_]);
}
}
// Checking the delta between the two extreme values
if (max_dep >= min_dep + 2)
return -1;
else if (max_dep == min_dep)
return 0;
// Processing DP on a tree
final_res = 0;
dfs(root, 1);
if (final_res < 0)
return -1;
return final_res;
}
} tdp;
int n;
int main(int argc, char** argv)
{
scanf("%d", &n);
tdp.root = 1;
tdp.n = n;
for (int i = 1, a, b; i <= n; i++) {
scanf("%d%d", &a, &b);
if (a != -1)
tdp.set_child(i, a, 0);
if (b != -1)
tdp.set_child(i, b, 1);
}
// Finished building tree.
int res = tdp.eval();
printf("%d\n", res);
return 0;
}