Description
在遥远的东方, 有一个神秘的民族, 自称 Y 族. 他们世代居住在水面上, 奉龙王为神. 每逢重大庆典, Y 族都会在水面上举办盛大的祭祀活动. 我们可以把 Y 族居住地水系看成一个由岔口和河道组成的网络. 每条河道连接着两个岔口, 并且水在河道内按照一个固定的方向流动. 显然, 水系中不会有环流 (下图描述一个环流的例子).
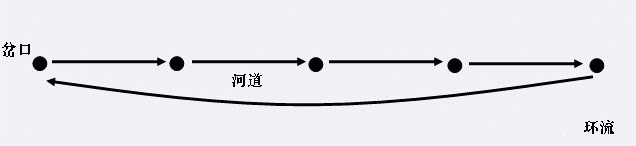
由于人数众多的原因, Y 族的祭祀活动会在多个岔口上同时举行. 出于对龙王的尊重, 这些祭祀地点的选择必须非常慎重. 准确地说, Y 族人认为, 如果水流可以从一个祭祀点流到另外一个祭祀点, 那么祭祀就会失去它神圣的意义. 族长希望在保持祭祀神圣性的基础上, 选择尽可能多的祭祀的地点.
Input
第一行包含两个用空格隔开的整数 \(n, m\), 分别表示岔口和河道的数目, 岔口从 \(1\) 到 \(n\) 编号.
接下来 \(m\) 行, 每行包含两个用空格隔开的整数 \(u, v\), 描述一条连接岔口 \(u\) 和岔口 \(v\) 的河道, 水流方向为自 \(u\) 向 \(v\).
Output
第一行包含一个整数 K, 表示最多能选取的祭祀点的个数.
Sample Input
4 4
1 2
3 4
3 2
4 2Sample Output
2Data Range
对于所有数据, 满足:\(n \leq 100, m \leq 1000\).
Explanation
首先用类似 Floyd 的做法预处理出两个点之间的联通情况.
如果两个点 \(i \rightarrow j\) 联通, 那么我们在二分图里连边 \((i, n+j)\).
然后针对二分图 \(G = (V, E), V = (\{1, 2, \ldots, n\}, \{n+1, n+2, \ldots, 2n\})\) 进行二分图匹配.
匹配出的是最多可以产生多少对联通的节点.
然后用 \(n\) 减去这个最大匹配数即为答案.
Source Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define rep(_var,_begin,_end) for(int _var=_begin;_var<=_end;_var++)
using namespace std;
typedef long long lli;
const int maxn = 1010, maxm = 10010, maxN = 110;
class BipartiteGraph
{
public:
struct edge
{
int u, v;
edge *next;
};
int n, ecnt;
edge *edges[maxn], epool[maxm];
void add_edge(int u, int v)
{
edge *p = &epool[++ecnt];
p->u = u; p->v = v;
p->next = edges[u]; edges[u] = p;
return ;
}
int from[maxn];
bool vis[maxn];
bool find(int p)
{
for (edge *ep = edges[p]; ep; ep = ep->next)
if (!vis[ep->v]) {
vis[ep->v] = true;
if (!from[ep->v] || find(from[ep->v])) {
from[ep->v] = p;
return true;
}
}
return false;
}
int eval(void)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
memset(vis, 0, sizeof(vis));
if (!from[i])
sum += (int)find(i);
}
return sum;
}
} graph;
int n, m;
bool lnk[maxN][maxN];
int main(int argc, char** argv)
{
scanf("%d%d", &n, &m);
for (int i = 1, a, b; i <= m; i++) {
scanf("%d%d", &a, &b);
lnk[a][b] = true;
}
// Maintaining connectivity
rep(k, 1, n) rep(i, 1, n) rep(j, 1, n)
lnk[i][j] |= lnk[i][k] && lnk[k][j];
// Inserting into graph
rep(i, 1, n) rep(j, 1, n)
if (lnk[i][j] && i != j)
graph.add_edge(i, n + j);
graph.n = n * 2;
// Running and getting result
int res = n - graph.eval();
printf("%d\n", res);
return 0;
}