| Problem Specification | Value |
|---|---|
| Time Limit | 1 Sec |
| Memory Limit | 162 MB |
| Submit | 4090 |
| Solved | 2256 |
Description
轮状病毒有很多变种, 所有轮状病毒的变种都是从一个轮状基产生的. 一个 N 轮状基由圆环上 N 个不同的基原子
和圆心处一个核原子构成的, 2 个原子之间的边表示这 2 个原子之间的信息通道. 如下图所示
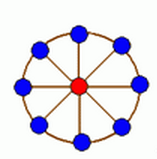
N 轮状病毒的产生规律是在一个 N 轮状基中删去若干条边, 使得各原子之间有唯一的信息通道, 例如共有 16 个不
同的 3 轮状病毒, 如下图所示
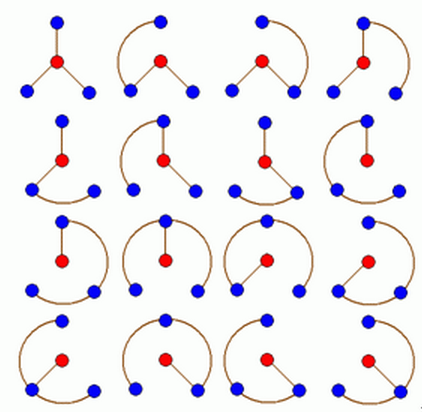
现给定 n (N<=100), 编程计算有多少个不同的 n 轮状病毒
Input
第一行有 1 个正整数 n
Output
计算出的不同的 n 轮状病毒数输出
Sample Input
3Sample Output
16HINT
Source
话说 基尔霍夫矩阵什么的就不提了, 证明太繁琐.
最后的结论是 f[i] = f[i - 1] * 3 + 2 - f[i - 2].
但是需要写一个高精度来做这道题. 由于不涉及乘法 (高精乘高精或高精乘大数), 所以乘法可以直接通过很少的多次加法来实现, 就省去了不少行数.
#include <iostream>
#include <iomanip>
using namespace std;
typedef long long lint;
const lint lmx = 10000000000000000ll;
class hprec { public: long long d[4];};
hprec mint(int _){hprec a;a.d[0]=_;a.d[1]=a.d[2]=a.d[3]=0;return a;}
hprec operator+(hprec a,hprec b){hprec c;for(int i=2;i>=0;i--){c.d[i]=a.d[i]+b.d[i];if(c.d[i]>=lmx)c.d[i]-=lmx,c.d[i+1]++;}return c;}
hprec operator-(hprec a,hprec b){hprec c;for(int i=2;i>=0;i--){c.d[i]=a.d[i]-b.d[i];if(c.d[i]<0)c.d[i]+=lmx,c.d[i+1]--;}return c;}
ostream& operator<<(ostream& _,hprec a){int f=1;for(int i=2;i>=0;i--){if(f&&a.d[i])_<<a.d[i],f=0;else if(!f)_<<setfill('0')<<setw(16)<<a.d[i];}return _;}
int main(int argc, char** argv)
{
hprec a = mint(0), b = mint(1);
int n; cin >> n;
for (int i = 1; i < n; i++) { hprec c = b + b + b + mint(2) - a; a = b; b = c; }
cout << b << endl;
return 0;
}from pydatagen import *
printf('%d\n', randrange(2, 101))
fclose()